2022년 6월 7일 수정: 이미지 파일의 크기를 줄였습니다.

겜스가 2.3으로 업데이트되면서 그래도 살만해졌습니다. 사실 겜스1을 쓰면서는 엔진과 언어가 너무 불편해서 겜스넘구데기를 연발했는데 구조체와 함수(생성자 함수도!) 문법이 생기면서 그나마 제가 편한 대로 코드를 짤 수 있게 되었네요.

그동안 제 돈으로 게임메이커 스튜디오 2를 구매하기는 부담스러워서 겜스1로 버티고 있었는데, 최근에 KGMC 교육잼에 도전하면서 (2번째로) 겜스2를 체험해볼 수 있었고 수상까지 해서 Desktop 라이선스도 받았습니다. 이런 큰 상품을 받고도 뭐라도 하지 않으면 죄책감이 들기도 하고 그동안 게임잼에 출품하면 후기를 쓰는 습관이 들었으니... 이 글에서는 날짜별로 허니하우스를 어디부터 어떤 방식으로 만들었는지 정리해 보려고 합니다. 혹시 안 해보셨다면 여기서 해보실 수 있습니다.

이 글에서 언급하는 모든 날짜는 개발하면서 찍어둔 동영상 등 파일 기록에서 유추해 작성했습니다. (많이 찍어놔서 다행이네요! 그럴 시간에 깃 커밋이나 해) 주로 야간에 작업하기 때문에 '10일'이라고 하면 9일 저녁부터 다음 날 밤까지를 의미하니 참고해 주세요.

사실은 원래 3월 말쯤에 올리려고 했는데 시험기간이 겹쳐서 한 달이나 늦었네요. 빨리 올리지 못해 죄송합니다 😅

1월 31일

허니하우스 프로젝트를 시작하고 처음 남긴 기록이네요. 보드 및 회전 코드를 구현했습니다. 아직 회전할 만한 게 없어서 시험 삼아 보드를 회전시켜봤습니다.

사실은 방금 그 "보드 및 회전 코드를 구현했습니다" 한 문장에 대해서 엄청나게 긴 해설을 쓰려고 합니다.

무턱대고 행렬부터 만들기

선형대수학은 행렬 몇 개를 곱해서 공간을 마음대로 조작할 수 있는(약간의 과장을 섞었습니다) 수학 분야입니다. 저 육각형 보드를 구현하는 데도 행렬을 유용하게 쓸 수 있을 거라고 생각했고 정확히 맞아떨어졌습니다. 물론 꼭 행렬을 써야 되는 건 아니니 겁먹으실 필요는 없지만... 일단 배워두니 편하게 구현할 수 있었습니다. 혹시 머릿속에 잘 안 들어간다면 마음 편하게 패스해 주세요.

허니하우스에서는 육각형 보드를 아래와 같은 2차원 배열로 표현합니다. 밑줄 _은 가독성을 위해서 0 대신 넣었고 빈 공간을 의미합니다.

board = [
	[2, 5, 3, 2, 1, _, _, _, _],
	[1, 1, 2, 5, 4, 5, _, _, _],
	[5, 4, 4, 1, 3, 2, 5, _, _],
	[2, 5, 3, 5, 2, 1, 4, 3, _],
	[5, 3, 5, 4, 4, 4, 4, 4, 3],
	[_, 2, 2, 4, 3, 1, 2, 1, 5],
	[_, _, 5, 2, 1, 2, 3, 1, 1],
	[_, _, _, 3, 4, 1, 1, 2, 2],
	[_, _, _, _, 4, 4, 3, 4, 5]
];

이 2차원 배열을 화면에 그릴 때 각 점의 좌표를 구해야 하는데, 이때 아래와 같은 3×3 배열을 만들어두면...

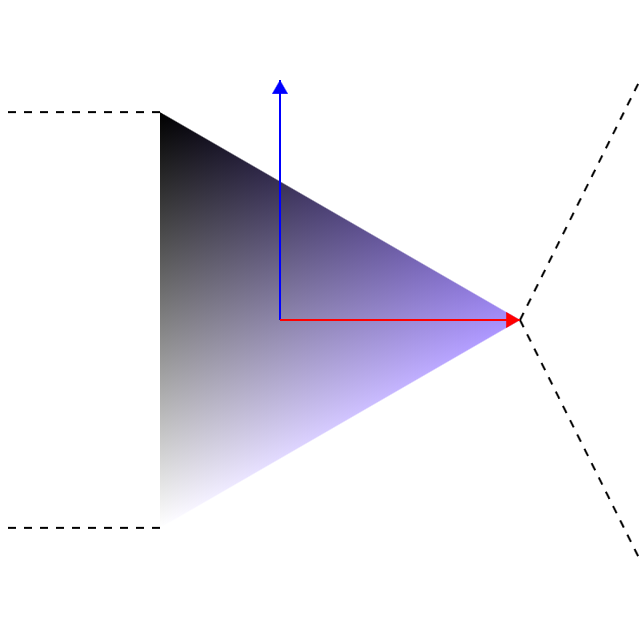
\[\boldsymbol{M} = \begin{pmatrix} a & c & x \\ b & d & y \\ 0 & 0 & 1 \end{pmatrix}\]

아래 사진과 같은 좌표계를 표현할 수 있게 됩니다. \((x, y)\)가 새로운 원점이고 빨간색 화살표가 \(x\)축 한 칸, 파란색 화살표가 \(y\)축 한 칸을 나타냅니다. 참고로 허니하우스에서 (거의) 모든 육각형은 아래처럼 "\(x\)축이 살짝 올라간" 좌표 체계로 다룹니다.

실제로 2차원 배열 좌표 board[y_from][x_from]에서 화면상의 좌표 \((x_{to}, y_{to})\)를 구하려면 주어진 좌표를 열벡터 \(\begin{pmatrix} x_{from} \\ y_{from} \\ 1 \end{pmatrix}\)로 바꾸고 왼쪽에 \(\boldsymbol{M}\)을 곱하기만 하면 됩니다. 이런 형태의 행렬 곱셈은 꽤 자주 쓰이기 때문에 아핀 변환이라는 이름이 따로 붙어 있습니다.

\[\boldsymbol{M} \begin{pmatrix} x_{from} \\ y_{from} \\ 1 \end{pmatrix} = \begin{pmatrix} x_{to} \\ y_{to} \\ 1 \end{pmatrix}\]

왜 굳이 행렬까지 만들어서 쓰나요?

고등학교 수학에서도 빠진 행렬을 굳이 복잡하게 쓰지 않아도 두 줄짜리 코드로 육각형 보드를 그릴 수 있긴 합니다.

x_to = a*x_from + c*y_from + x;
y_to = b*x_from + d*y_from + y;

그런데 이런 식으로 코드를 짜면 행렬 2개 대신 느닷없이 변수 a, b, c, d, x, y, x_from, y_from, x_to, y_to(무려 10개!)를 머릿속으로 전부 저글링해야 합니다. 저 식을 무언가 좌표 변환이 필요할 때마다 입력해야 한다면 귀찮기도 하지만 값을 잘못 입력할 일도 많아집니다. 그동안 게임 개발을 여러 번 해보니까 차라리 준비 코드를 길게 쓰더라도 (대충 좌표 변환하는 행렬)과 (대충 변환하고 싶은 열벡터)만 머릿속에 넣어두는 게 편하더라고요. 값뿐만 아니라 연산의 관점에서도 위에 있는 곱셈 4번 덧셈 4번짜리 코드보다 (행렬의) 곱셈 1번이 훨씬 간단하고요.

코드를 확인해 보자

사실 별건 없고 constructor 함수 안에 그냥 필요한 연산만 이것저것 static으로 정의해놓은 형태입니다. 꽤 간단한 구조이지만 관련된 메소드를 전부 Matrix 안으로 욱여넣을 수 있어서(생각할 게 줄어든다는 의미입니다) 개인적으로 constructor 문법을 좋아하는 편입니다.

// 구조만 보려고 하는 거니까 구현 어떻게 했는지는 생략할게요

function Matrix(h, w) constructor {
	static
		height = function() { /* 행 개수 */ },
		width = function() { /* 열 개수 */ },
		plus = function(rhs) { /* self + rhs인데 실제로 쓰진 않았네요 */ },
		negated = function() { /* -self */ },
		times = function(rhs) { /* self*rhs (rhs는 행렬) */ },
		inverse = function() { /* self의 역행렬 */ },
		affine = function(_x, _y) { /* 아핀 변환 (2×2, 3×3 행렬이어야 함) */ };
	
	data = new_2d_array(h, w); // h×w짜리 0으로 채워져 있는 2차원 배열
}

function matrix_identity(size) { /* size×size짜리 단위행렬 */ }
function matrix_from(array) { /* ... */ }
/*
matrix_from([
	[1, 2],
	[3, 4]
])
을 하면 행렬
[1 2]
[3 4]
를 만들 수 있습니다.
*/

이 중에서 역행렬을 구하는 알고리즘은 원래 구현하기 어려운데, 어차피 2×2나 3×3 행렬만 쓸 거라서 하드코딩을 했습니다.¹

회전도 행렬로

아까 "행렬로 좌표계를 표현할 수 있다"는 뉘앙스로 얘기했는데, 좌표계 표현 말고도 기존의 좌표계에 변환을 가하는 데 쓸 수 있습니다. 예를 들어 아래 조각을 시계 방향으로 60도 회전하는 경우를 생각해 봅시다.

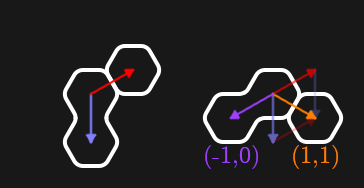
핵심만 이야기하자면, 원래 \((1, 0)\)과 \((0, 1)\)이었던 점이 어떤 점으로 변환되는지 구하면 그 변환을 나타내는 행렬도 구할 수 있습니다. 여기서는 \((1, 0)\)은 \((1, 1)\)로, \((0, 1)\)은 \((-1, 0)\)으로 변환되니 구하는 행렬은

\[\boldsymbol{R} = \begin{pmatrix} 1 & -1 \\ 1 & 0 \end{pmatrix}\]

로 나타낼 수 있습니다. 실제로 \(\boldsymbol{R} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \end{pmatrix}\), \(\boldsymbol{R} \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} -1 \\ 0 \end{pmatrix}\)이 되는 것을 확인할 수 있습니다.

검산을 위해 Wolfram|Alpha로 \(\boldsymbol{R}^6\)을 계산하는 과정을 거쳤습니다. \(\boldsymbol{R}^n\)은 \(\boldsymbol{R} \boldsymbol{R} \cdots \boldsymbol{R}\), 즉 변환 \(\boldsymbol{R}\)을 연속으로 \(n\)번 수행한다는 의미이고, 60도 회전을 6번 하면 원래대로 돌아오니 "아무 변환도 안 함" 행렬인 \(\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\)이 나와야 합니다.

유레카! 실제로는 회전할 때 원점도 같이 돌아가는 문제 때문에 아무 생각 없이 행렬 하나를 곱하는 것보다는 복잡한 처리를 했습니다.

그... 첫날치고 꽤 길고 어려운 얘기를 해버렸네요. 요약하자면 "행렬로 기본 기능을 몽땅 구현했다"가 되겠습니다.

2월 1일

마우스로 플레이하는 게임이니 마우스가 어느 칸에 있는지도 판정해야겠죠. 생각보다 아이디어를 떠올리기가 어려웠고 버그도 많이 났었습니다.

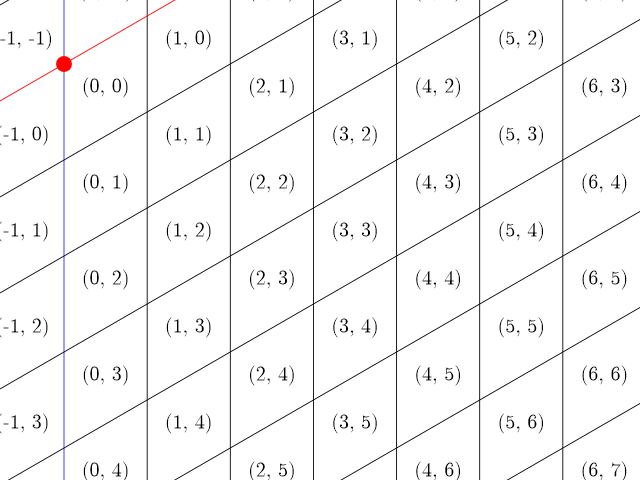
저는 마우스가 그리드에서 어떤 칸에 있는지를 구하고(아래 이미지 참고. 역행렬을 이용했습니다), 그 칸에 걸친 점 4개 중 마우스와 가장 가까운 것을 찾는 방식으로 구현했습니다. 원래 육각형 보드니까 삼각형으로 자르려고 했는데 역시 어렵더라고요.

2월 2일

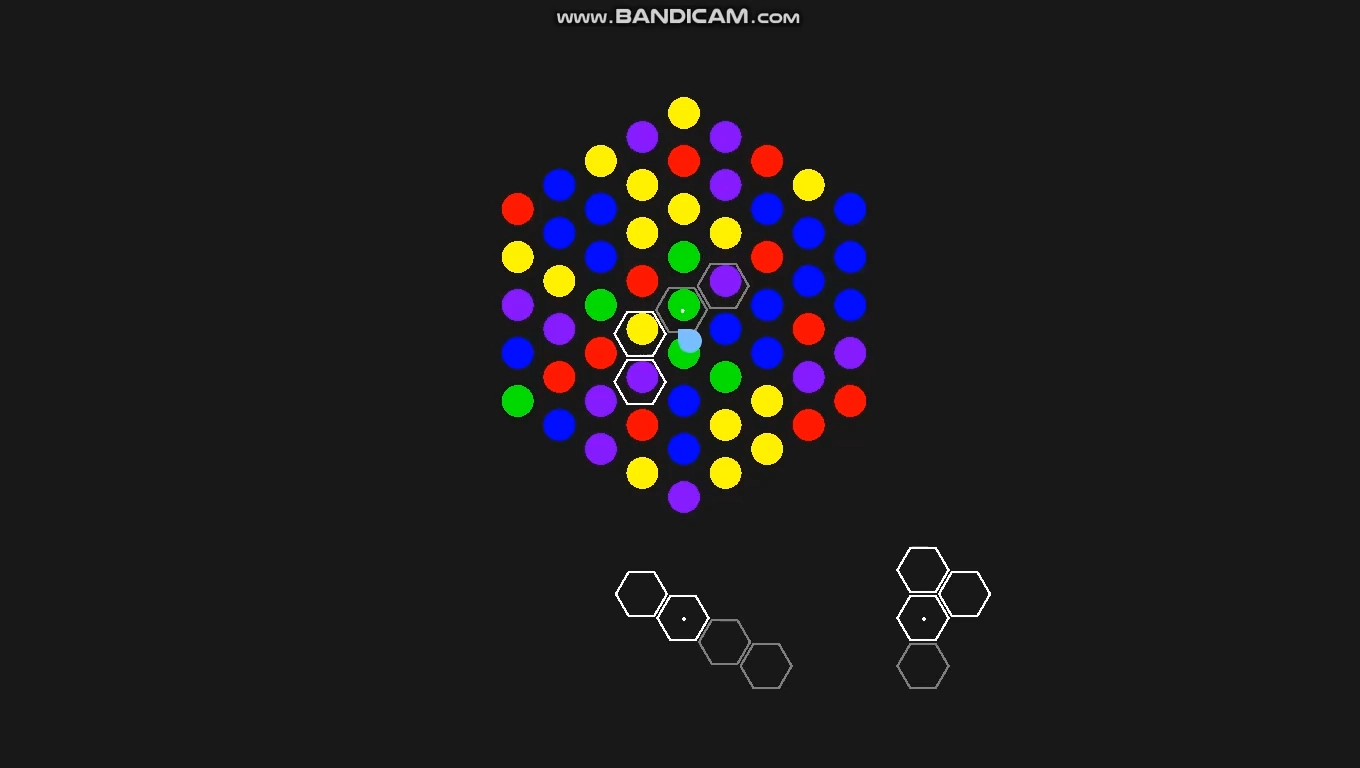
기본적인 조각 기능을 구현했습니다. 실제로 매치는 되지 않지만 회전, 뒤집기, 마우스 클릭 판정 정도가 가능하고, 완전하지는 않지만 보드 위에 올리면 가까운 칸에 스냅이 됩니다.

조각 표현은 두 가지 방법으로 할 수 있는데, 하나는 아래와 같이 2차원 배열로 표현하는 방법이고...

// 위 사진에서 가장 오른쪽의 조각은 다음과 같이 표현됩니다. 이 코드에서도 _을 0 대신 사용합니다.

example_piece_1 = {
	origin: [1, 0], // y, x 순서
	data: [
		[1, _],
		[1, 1],
		[2, _]
	]
};

다른 하나는 각 조각마다 그 위치와 색상을 적어두는 방법입니다.

// 같은 조각을 다른 방식으로 표현한 결과입니다.
example_piece_2 = [
	{ x: 0, y: -1, gray: false },
	{ x: 0, y: 0, gray: false },
	{ x: 1, y: 0, gray: false },
	{ x: 0, y: 1, gray: true }
];

전자는 직관적이지만 회전 등 내용물을 순회하는 연산이 느리고(빈 칸에도 연산해야 하기 때문에), 후자는 공간을 적게 차지하는 조각에서 효율적이지만 그리는 연산이 비교적 무겁습니다(주변 타일에 따라 다른 텍스처를 쓰기 때문에). 개발 초반에 별 고민 없이 전자로 결정했지만, 아무래도 후자는 구조체를 많이 만들고 그리기 연산을 1초에 180번씩(1초에 60프레임, 한 프레임당 조각 3개) 해야 되는 걸 생각하면 아마 옳은 결정이었을 겁니다.

2월 3일

실제로 조각을 매치할 수 있게 되었습니다.

디스코드에 올렸던 "공포의 4중 포문" 글도 바로 이 조각 매치 로직이었습니다. 코드를 전부 보여드릴 수 없어서 4중 for문이라고 둘러댔는데, 사실은 7중 for문이었습니다. 도대체 뭘 하길래 7중 for문이냐고요?

• 조각 3개를 순회하는데 한 겹
• 모든 각도로 체크하는데 한 겹
• 뒤집은 조각으로 체크하는데 한 겹
• 보드상의 모든 위치를 순회하는데 두 겹
• 조각의 모든 칸을 체크해야 되기 때문에 두 겹

물론 한 곳에서 7중 for문을 전부 돌리는 건 아니고 for문을 돌리는 함수를 호출하는데 그 함수가 또 for문을 돌리고... 형태이긴 합니다. 3중도 4중도 아닌 7중이니 죄책감도 꽤 들었지만 결과적으로는 제 할일을 하고 게임이 느려진 것도 아니니² 장땡이라고 생각합니다.

2월 7일

나흘 동안 실제 게임에 사용할 그래픽 리소스를 만들고 적용했습니다. 덤으로 밝은 모드(?)와 (색약/색맹 플레이어를 위한) 무늬 켜기/끄기 버튼도 만들었습니다. 분명 접근성으로 넣은 요소였는데 개발하다 보니까 오히려 무늬가 없는 게 안 익숙하네요.

배경과 글꼴과 잇창명 로고 빼고 모든 그래픽을 SVG로 만들었을 만큼 SVG를 애용했습니다. 제가 그래픽까지 코드로 만드는 게 편할 정도로 코드를 자주 쓰는 특이한 사람이니까 무서워하지 말아주세요.

조각이 조각조각

이때 즈음에 조각으로 무엇을 넣을까(최대 몇 칸이 들어가게 할까, 최대 몇 구획으로 나눌까 등)를 고민했는데 결국에는 가능한 모든 3~5칸짜리 조각을 1~2구획해서 넣었습니다. 모든 조각 종류는 영문 위키백과의 Polyhex (mathematics) 문서를 참고했고 구획은 눈으로 직접 보고 나눴습니다. 빠진 게 있으려나 모르겠네요.

이렇게 해서 넣은 조각 수가 무려 131종류나 되는데 그 그래픽은 어떻게 그렸냐면... 조각의 주변 배치에 따라 가능한 모든 경우의 수를 이미지 1장씩으로 만들고 모든 칸에 그려서 합쳤습니다. 지금 생각해보면 131종류나 되는 조각을 전부 입력하는 것 다음으로 끔찍한 노가다였던 것 같네요.

공장식 버튼 만들기

2월 7일 기록에 처음으로 UI 요소가 등장했네요. 이후로도 저런 형태의 버튼을 많이 만들 것 같아서 미리 객체로 만들어두고 변수 몇 개만 건드려도 기본 기능이 돌아가도록 했습니다.

버튼 객체에서 조작할 수 있는 것들로는...

• x, y
• sprite_index
• image_index (image_speed를 0으로 맞춰 놓았습니다.)
• 색상
• 마우스를 올리면 나오는 문구
• 마우스를 올렸을 때 문구가 나오는 방향 (fa_right, fa_middle 등을 재활용했습니다.)
• 마우스 올라감 판정 함수
• 눌렸을 때 실행할 함수

정도로 기억하고 있습니다. 처음에는 이것과 조금 달랐고 개발하면서 조금씩 수정했습니다. 이외에 스프라이트가 체크박스인 경우를 인식해서 문구가 항상 표시되고 체크박스 대신 글씨를 눌러도 눌린 것으로 인식하는 추가 기능도 있습니다.

2월 8일

3종류의 게임 모드 버튼과 그 버튼에 쓸 이미지를 넣었습니다. 아직 실제로 작동하지는 않았고, 이후 구현하기 쉬워 보이는 순서대로 차례차례 넣게 되었습니다.

2월 9일

작은 크기의 보드와 재시작 버튼을 구현했습니다. 아무래도 보드가 작다 보니까 너무 빨리 죽어서 밸런스 조절을 하기로 했었는데 정확히 언제 조절했는지는 기억이 안 나네요.

2월 11일

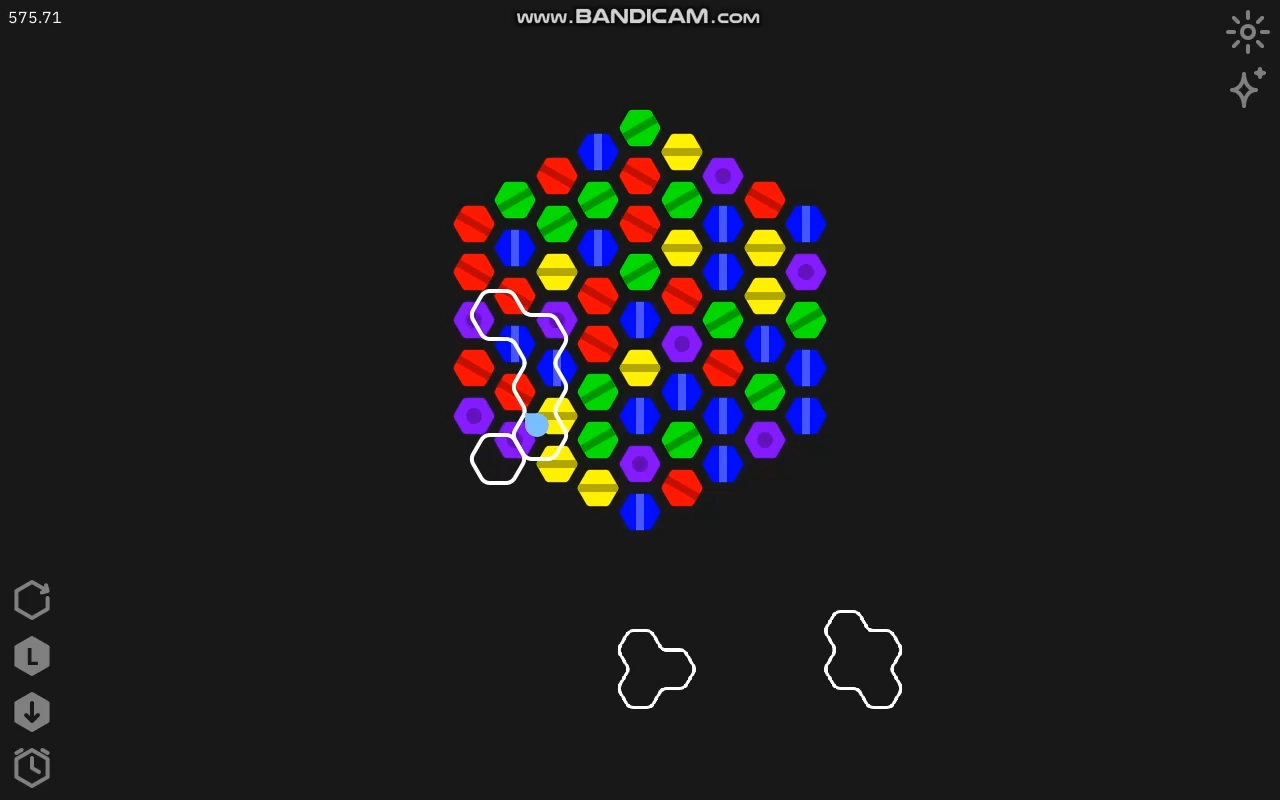
중력 모드를 구현했습니다. 스크린샷으로 찍은 보드 상태를 보면 아시겠지만... 아직까지도 게임 오버 판정은 구현이 안 돼있었습니다.

2월 14일

무관하지만 이날은 제 생일이었습니다. 🥳

Windows API의 색상 선택 창(이미지 출처)을 살짝 빌려서 색 조합 편집 기능을 추가했습니다. 무늬 설정은 아직 구현하지 않았습니다. 이전에 대충 만들었던 무늬들도 개수가 적고 마음에 들지 않아 새로 여러 개 만들었습니다.

"Windows API"에서 짐작하셨겠지만, DLL을 직접 만들어서 GMS2 확장으로 넣었습니다. 사실 둘 다 이때 처음 해봐서 삽질을 꽤 했습니다. 나중에 다시 언급하겠지만 지인분께 테스트를 부탁했더니 창이 안 나온다고 해서 DLL 확장을 버렸습니다. 😱

버튼이 넘쳐흘러

이때부터 버튼이 본격적으로 많아지기 시작하면서(벌써 16개예요!) 뭔가 잘못될 조짐을 느끼고 수많은 버튼을 효율적으로 관리하기 위해 웹 개발을 하던 기억을 떠올려서 버튼 관리 시스템을 만들기로 했습니다. 정확한 날짜가 기억나지는 않는데 중간에 빌드했던 파일을 열어서 확인해보니 확실히 21일까지는 완성했었습니다.

버튼이 들어갈 수 있는 계층을 여러 개 만들어두고 사용자의 동작("설정 버튼을 누름" 등)에 따라 한 층씩 넣거나 빼는 방식입니다. 가장 위층에 있는 버튼만 누를 수 있고, 나머지는 마우스가 올라오거나 눌러도 반응하지 않습니다. 이렇게 만들어두면 기존의 마우스 이벤트는 쓸 수 없게 되니 버튼마다 onclick(클릭했을 때 호출할 함수)이나 hover_check(마우스 올라감 판정 함수) 등의 인터페이스 함수를 만들고 이벤트 대신 썼습니다. 설정 창을 열었을 때 배경을 흐리게 만들려고 GMS2 레이어도 몇 개 만들었습니다.

코드 들춰보기

GMS2에서 제일 비직관적인 게 함수 바인딩(함수 내에서 self가 무엇을 가리키는지)이었습니다. yellowafterlife님의 블로그에서 설명을 읽어보긴 했는데 뭔가 안 맞는 게 있었던 것 같고(제가 잘못 읽어서 그럴 수도 있긴 해요) 그냥 메소드를 만들 때마다 method로 포장했습니다...

interface = {
	hierarchy: [
		{ // { ... } 하나가 계층 하나입니다.
			onblur: function() {
				// 클릭했는데 아무것도 안 눌렸을 때 실행되는 기본 동작
			},
			items: [
				// 실제 버튼 객체들...
			]
		},
		// ...
	],
	pressed: undefined,
	focused: undefined,
	refs: {
		// onclick에서 다른 버튼 조작하려고 만들어놓은 구조체
	}
};
interface.focusing = method(interface, function(mx, my) {
	// 마우스가 (mx, my)에 있을 때 무슨 버튼이 포커스 상태인지 찾는 함수
	// interface.hierarchy[가장 끝에 있는 거].items를 순회합니다.
});
interface.onmousedown = method(interface, function(mx, my) {
	// 마우스 버튼을 누른 순간 실행되는 함수
	// 무슨 버튼이 눌렸는지는 interface.focusing으로 체크합니다.
});
interface.onmouseup = method(interface, function(mx, my) {
	// 마우스 버튼을 뗀 순간 실행되는 함수
});

2월 15일

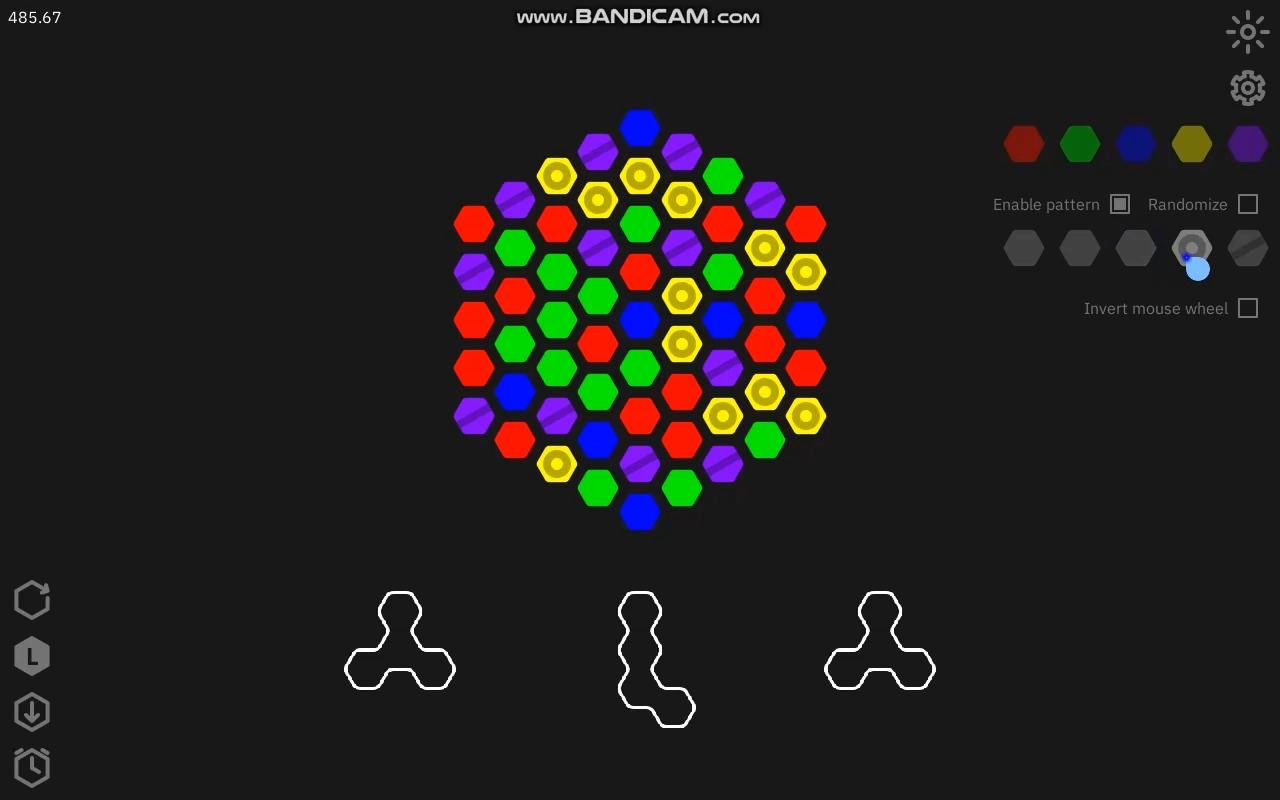
체크박스와 무늬 설정을 구현했습니다. 덤으로 마우스 휠 방향을 바꾸는 체크박스까지 만들었습니다.

2월 16일

보드 위에서 새로운 칸이 내려오는 애니메이션을 만들었습니다. 부드러운 게 좋네요. 원래 디스코드에 근황으로 올리면 어떨까 싶어서 움짤로 찍어봤는데 결국에는 안 올리고 트위터에만 올렸습니다.

2월 18일

드디어 게임 오버를 구현했습니다!!! 최종본과는 달리 게임 오버 조건을 만족하면 왜 죽었는지 볼 시간도 안 주고 바로 사라지는 애니메이션으로 넘어갔습니다.

게임 오버 애니메이션은... 그냥 모든 칸에 무작위로 시각을 넣어두고 각각 그 시각이 지나면 사라지게 만들어서 구현했습니다.

2월 20일

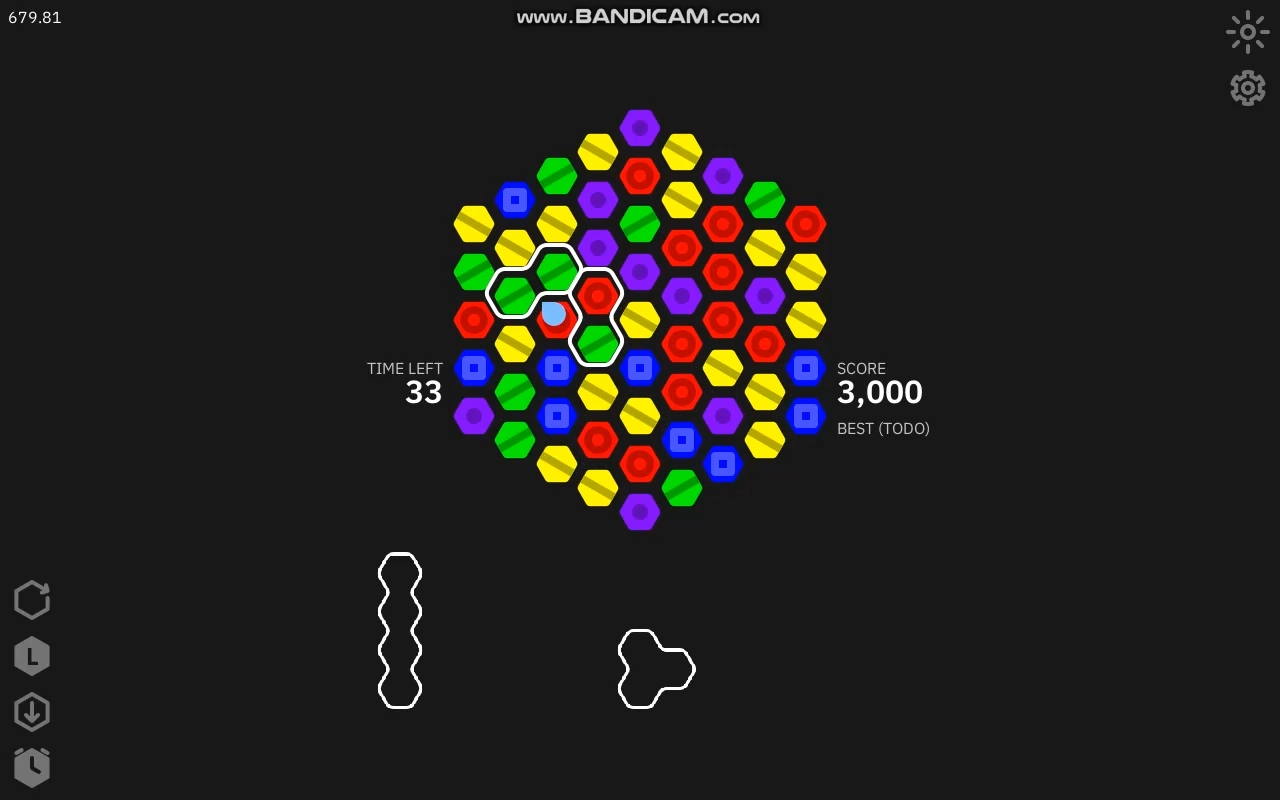
시간 제한 모드를 실제로 구현했습니다. 이때는 아직 60초 모드밖에 없었고 보드를 섞기 전에 아무런 신호도 주지 않았습니다. 시간 제한 UI를 구현해야 하길래 점수도 얼레벌레 구현했습니다.

점수 시스템을 어떻게 설계할지 고민을 많이 했습니다. "짧은 시간 안에 연속으로 맞추면 보너스를 줘라" 같은 조언도 어느 정도 들었는데 결국에는 순수하게 매치한 조각 종류만 점수에 반영되게 했습니다.

조각 종류별로 점수도 어떻게 매길지 고민했는데, 제가 체감한 매치 난이도별로 (+ 전체 칸 수가 많고 한 종류의 칸 수가 많을수록 어렵다는 경험 법칙에 의해) 점수를 매겼습니다.

• 2칸 + 1칸: 150점
• 2칸 + 2칸: 400점
• 3칸: 300점
• 3칸 + 1칸: 400점
• 3칸 + 2칸: 800점
• 4칸: 900점
• 4칸 + 1칸: 1000점
• 5칸: 2700점

개인적으로 게임을 하는데 부담이 느껴지는 걸 싫어하는 성향이라 처음부터 시간제한 모드를 염두에 두지는 않았었는데, 막상 해보니 생각보다 많은 걸 느꼈습니다.

• 무한 모드는 의외로 운이 나빠서 죽는 경우가 많은데, 시간제한 모드는 일단 60초 동안 안 죽고 할 수 있어서 좀 더 공평해 보인다.
• 60초는 너무 촉박한 것 같다. 120초 모드도 있었으면 좋겠다.
• 한 번 안 보이기 시작하면 당황해서 망하는 것 같으니 힌트가 있었으면 좋겠다.
  • 나중에 이걸 구현하느라 게임 오버 로직도 건드렸습니다.

2월 21일

이날 처음으로 exe 빌드를 만들어서 Slumbone님께 테스트 플레이를 부탁드렸고 컬러 피커 창이 안 나오는 걸 포함해서 버그 2개를 찾아주셨습니다. 이외에도 귀중한 피드백을 많이 받았습니다.

2월 22일

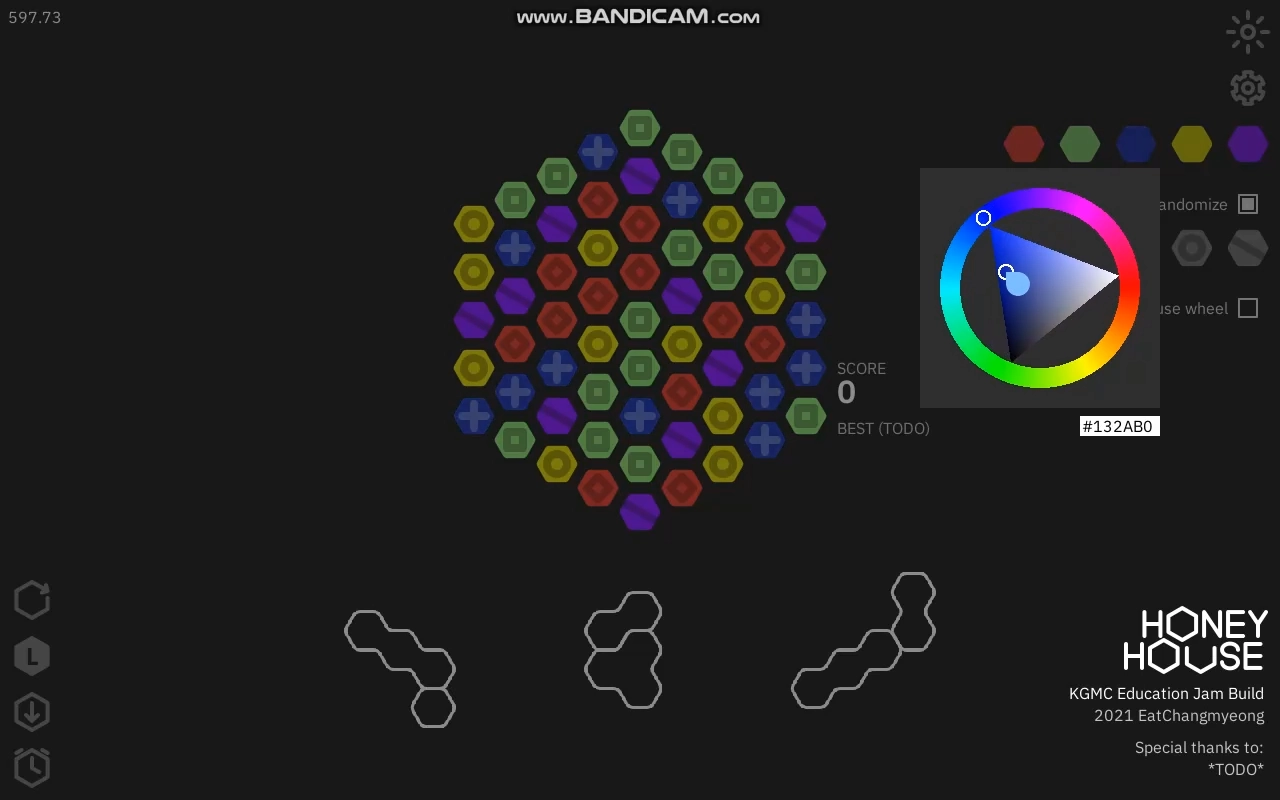
하루 만에 DLL을 버리고 GMS2 컬러 피커 구현체를 만들었습니다. 🏃 덤으로 힌트 기능도 만들었습니다.

무슨 컬러 피커?

사실 지금 구현된 대로 색상환 + 회전하는 삼각형 컬러 피커와 텍스트 입력창 조합으로 결정한 건 덜 심심하다(...)는 걸 제외하면 큰 이유가 없습니다. 그 대신 여러 이유로 선택지에서 배제한 컬러 피커 디자인은 있습니다.

아래 리스트의 모든 이미지는 User Experience Stack Exchange에 올라온 이 질문에서 가져왔습니다.

• 정해진 색 중 선택: 사용 경험 면에서 낫다는 의견을 봤지만(바로 위에 링크한 그 질문이 맞습니다) 버튼 수십 개가 필요해 보이길래 황급히 뺐습니다. 노가다는 조각 입력과 조각 그래픽으로 충분합니다...
• 사각형 + 슬라이더
• 가운데가 흰색인 색상환 + 슬라이더: 처음 보는 형태라서 머릿속에 잘 안 남기도 했고 비직관적이라서 뺐습니다.
• 색상환 + 사각형
• 색상환 + 삼각형
• 색상 코드 입력창: 저는 테마색이 정확히 #ab94fc여야 하는 사람이라서 무조건 넣기로 했습니다.

행렬을 잊지는 않았겠지

네, 또 행렬을 썼습니다. 색상환 부분은 당연히 아니고 안쪽에 있는 삼각형 부분입니다.

색상환을 기반으로 한 컬러 피커는 HSV 혹은 HSB 색 공간과 밀접한 관련이 있습니다(철자가 다르지만 둘 다 같은 개념입니다). 역시 자세한 설명은 생략하고 얘기하자면 H는 색상환 부분에 의해 완전히 결정되고, 안쪽의 세 꼭짓점 중 검은색은 V=0³, 흰색은 S=0, V=1, 원색은 S=1, V=1입니다.

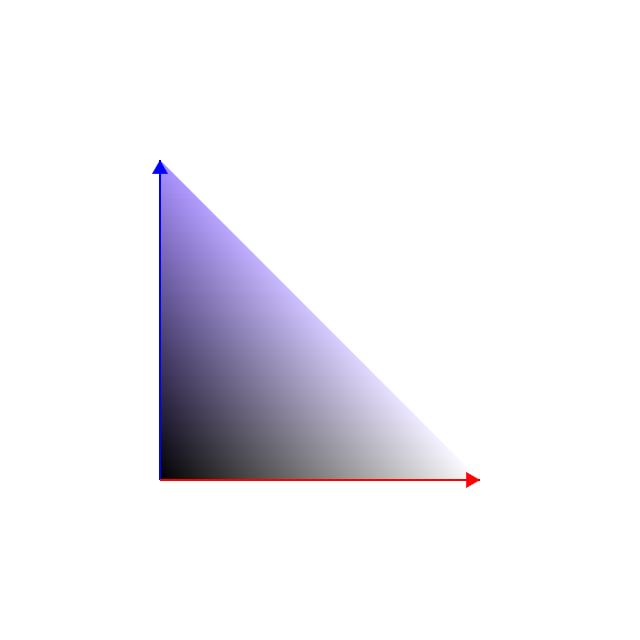
삼각형 부분의 좌표를 구하는 것이 문제인데, (당연히 행렬을 이용해서) 아래 그림과 같은 각도와 크기로(즉, 원색 꼭짓점이 (1, 0)에 오도록) 정규화했습니다. 마우스로 드래그하면서 삼각형 밖으로 나갔을 수 있기 때문에, 삼각형 내부의 가장 가까운 점을 찾아서 그쪽으로 넣는 과정을 거쳤습니다.

1. 마우스가 왼쪽에 점선으로 표시한 부분에 있을 경우 왼쪽 모서리 위에 오도록 이동한다. 이때 \(y\)좌표는 유지하고, \(x\)좌표만 바꾼다.
2. 마우스가 오른쪽에 점선으로 표시한 부분에 있을 경우 좌표가 오른쪽 꼭짓점과 같도록 이동한다.
   • 이 부분은 정확히 1번에서 처리하지 못하는 부분과 같도록 하였다.
3. 모든 모서리에 대해 위 과정을 반복한다. 이때 처리를 편하게 하기 위해 삼각형을 돌린다.

조금 복잡해 보일 수는 있지만, 이곳에 있는 데모처럼 \(x\)좌표와 \(y\)좌표를 따로 처리하는 것보다 직관적인 결과를 보여줍니다.

좌표를 삼각형 안으로 넣은 뒤에는 검은색 꼭짓점이 (0, 0), 흰색 꼭짓점이 (1, 0), 원색 꼭짓점이 (0, 1)로 오도록 변형했습니다. 여기까지 오면 \(S=\frac{y}{x+y}\), \(V=x+y\)를 이용해 색상을 구할 수 있습니다. 물론 0으로 나누기 처리도 해야 합니다.

지금 생각해보면 (0, 0), (1, 0), (0, 1) 대신 (0, 0), (0, 1), (1, 1)을 쓰는 게 나았겠다는 후회가 있긴 합니다. 이때는 식이 \(S=\frac{x}{y}\), \(V=y\)로 더 간단해집니다.

색상 코드 입력창을 만들고 GUI 컬러 피커 및 설정 버튼과 상호작용을 시킨 뒤에 빈 곳을 누르면 사라지도록 하면 컬러 피커가 완성됩니다. 꽤 밀도가 높았네요!

흰색 혹은 검은색

컬러 피커를 잘 보면 현재 선택한 색이 고리 모양으로 강조되어 있는데, 주변 색에 따라 흰색이 되기도 하고 검은색이 되기도 합니다. 잘 생각해보면 육각형 무늬도 주변 색에 따라 밝은 색이기도 하고 어두운 색이기도 했습니다.

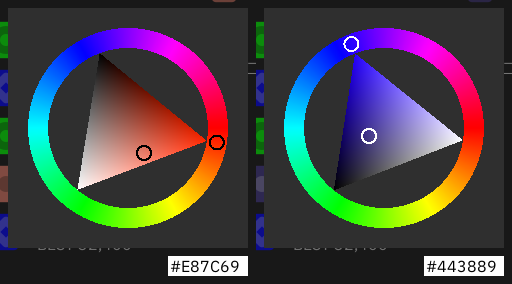
중요한 그래픽이 주변 색에 묻히면 안 되기 때문에 색상 대비를 계산해 가장 도드라져 보이는 색을 선택했습니다. 이 게임에서는 WCAG 2.1에서 Contrast Ratio의 정의⁴를 사용했습니다.

비교하려는 두 색의 상대적 밝기(relative luminance)가 각각 \(L_1\), \(L_2\) (단, \(L_1 \ge L_2\))일 때, 색상 대비 비(contrast ratio) \(CR\)은 다음 식으로 계산합니다.

\[CR = \frac{L_1 + 0.05}{L_2 + 0.05}\]

이때 sRGB 색 공간에서 빨강, 초록, 파랑 성분이 각각 \(R\), \(G\), \(B\) (단, \(0 \le R, G, B \le 1\))인 색의 상대적 밝기 \(L\)은 다음 식으로 계산합니다. \(G'\)와 \(B'\)의 계산식은 \(R'\)과 같으므로 생략합니다.

\[L = 0.2126R' + 0.7152G' + 0.0722B'\] \[R' = \begin{cases} \frac{R}{12.92} & \mbox{if } R \le 0.03928 \\ \left( \frac{R + 0.055}{1.055} \right)^{2.4} & \mbox{otherwise} \end{cases}\]

위 식을 (색 공간을 고려하지 않고) 코드로 옮기면 다음과 같습니다.

function contrast_ratio(lhs, rhs) {
	var
		l1 = relative_luminance(lhs),
		l2 = relative_luminance(rhs);
	return l1 > l2
		? (l1 + 0.05)/(l2 + 0.05)
		: (l2 + 0.05)/(l1 + 0.05);
}
function relative_luminance(color) {
	static f = function(x) {
		return x <= 0.03928
			? x/12.92
			: power((x + 0.055)/1.055, 2.4);
	};
	var
		r = colour_get_red(color)/255,
		g = colour_get_green(color)/255,
		b = colour_get_blue(color)/255;
	return 0.2126*f(r) + 0.7152*f(g) + 0.0722*f(b);
}

깨알같은 로고

게임 로고는 기록상 11일부터 고민하기 시작해 21일에 완성했고, 시작 화면과 크레딧 위치(설정 화면 오른쪽 아래)에 같이 넣었습니다.

트위터에서 여러 가지 로고를 두고 고민하다가 husua님이 제안해주신 육각형 3개짜리 로고로 결정했고, 여기에 박재민님이 "시작할 때 육각형 위에 조각으로 매치하게 하자"는 아이디어를 제안해 주셔서 시작 화면에 적용했습니다.

2월 28일

25일에 Slumbone님께 컨택을 해서 효과음을 부탁드렸고 28일에 실제로 받아서 적용했습니다.

원래 매치 소리와 5초 남았을 때 효과음만 부탁드리려고 했는데 어쩌다가 시간 초과 효과음과 클릭음까지 받아버렸습니다. 아무래도 너무 친절하신 분 아닌가 하는 생각이 드네요. 🙇‍♂️

게임 내에서 음높이만 다른 효과음을 들어볼 수 있는데, 실제 음원 파일은 1개고 audio_sound_pitch(index, pitch)를 써서 음높이만 수정했습니다. 진동수 배수 방식을 쓰길래 평소에 주워들었던 관련 지식을 써먹었습니다(\(n\)옥타브 높게 하려면 pitch = power(2, n), \(n\)반음 높게 하려면 pitch = power(2, n/12)).

이 정도로 날짜가 기억나는 것들은 모두 정리했습니다. 아직 남은 게 있긴 한데...

남은 작업들

리팩토링

2월 20일쯤으로 기억하고 있습니다. 오브젝트 안에 변수가 난잡하게 널브러져 있길래 남은 시간 동안 코드가 꼬일 것을 우려해서 메인 코드를 다시 짰습니다.

리팩토링은 주로 용도가 비슷하거나 비슷한 기능을 담당하는 변수를 한 구조체로 몰아넣는 방식으로 진행했습니다. 예를 들어 게임 진행에 필수적인 변수를 game 안에 몰아넣으면 게임판을 초기화할 때 무슨 변수를 건드려야 할지 훑기가 편해지고, 아니면 더 나아가 game 자체를 새로 만든 구조체로 갈아끼울 수도 있게 됩니다.

지금까지 쓴 코드의 80%~90%를 건드리는 작업이었던 만큼 시간도 오래 걸리고 실수도 많았지만 결과적으로는 문제 없이 끝냈습니다. 사실은 버그픽스가 예상보다 빨리 끝나서 "왜 버그가 또 안 생기지???" 하고 불안해하기도 했습니다.

점수 저장하기

세이브와 로드는 꽤 복잡해질 것 같아서 가장 나중으로 미뤘습니다. 이것보다 더 늦게 건드린 게 시작 화면과 사운드였습니다.

허니하우스의 세이브 포맷을 뜯어보면 이런 모습입니다. 세이브 파일 위치는 %localappdata%\honeyhouse\honeyhouse.save이고 모드별 점수와 (중간에 게임을 종료했다면) 보드의 상태가 들어 있으며, 이외에도 같은 폴더에 설정만 저장하는 settings.txt가 있습니다.

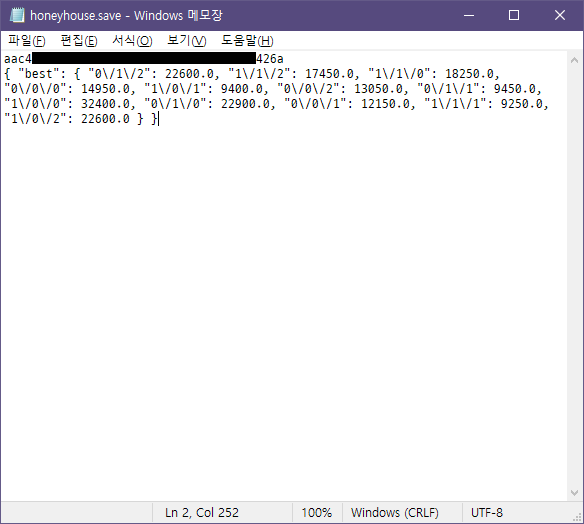
세이브 데이터는 마음 편하게 json_stringify를 써서 저장했습니다. 거의 완성된 이때의 허니하우스에는 총 12종류의 모드(보드 크기 큼/작음, 중력 켜짐/꺼짐, 시간 제한 없음/1분/2분)가 있었고, 각 모드를 구조체 키로 어떻게 표현할까 하다가 나온 방법이 위에서 볼 수 있듯이 0/0/2(보드 크기 0, 중력 0, 시간 제한 2라는 의미)와 같은 형태입니다.

건드리지 마세요

그런데 맨 윗줄에 (보안을 위해 가리긴 했지만) 정체모를 문자열이 추가로 저장되어 있네요. YoYo Games 블로그에는 HMAC을 사용해서 세이브 파일 변조를 방지하는 방법을 다룬 글이 있습니다(영어지만 읽기 좋고 재밌습니다!). 지난번에 트위터(로 기억하고 있습니다)를 통해 이 글을 눈여겨본 적이 있었고, 이번 기회에 구현해보기로 한 것입니다.

중요한 데이터를 저장할 때 그 데이터가 올바른지를 검증할 목적으로 체크섬을 포함하는 경우를 자주 볼 수 있습니다. 체크섬 함수 \(C(x)\)가 있다고 하면 \(x\)와 \(c=C(x)\)를 같이 저장해놓고 나중에 \(C(x)\)와 \(c\)를 비교해 다르다면 데이터 \(x\)가 손상됐든지 변조되었음을 감지할 수 있습니다.

이 체크섬 확인을 우회하면서 데이터 \(x\)를 \(y\)로 바꾸려면 다음과 같은 방법을 사용해야 합니다.

• 함수 \(C\)를 알고 있다면, 데이터와 \(c=C(y)\)를 둘 다 변조한다.
• 함수 \(C\)를 몰라도 \(C(x)=C(y)\)인 것만 확인할 수 있다면, 데이터만 \(y\)로 변조할 수 있다.

이 두 공격을 모두 방어하려면 다음 조건이 필요함을 알 수 있습니다.

• 공격자가 \(C\)를 모르거나 추측하기 매우 어려워야 한다.
• \(C(x)=C(y)\)인 \(y\)를 찾기가 불가능하거나 매우 어려워야 한다.

후자를 만족하는 함수로 가장 쉽게 찾을 수 있는 것이 암호학적 해시 함수입니다. 비밀번호 저장 등에도 사용할 수 있는 쓰임새 많은 함수라 GMS2에서도 지원하고 있는데, 자주 쓰이는 암호학적 해시 함수는 몇 가지 없기 때문에(당장 GMS2에도 MD5와 SHA-1밖에 없습니다) 전자를 만족하지는 않습니다.

HMAC으로는 (간단히 말해서) 해시 함수와 아무 문자열을 가지고 새로운 해시 함수를 만들어낼 수 있습니다. 문자열이 다르면 해시 함수도 달라지기 때문에 이 방법으로 전자도 만족시킬 수 있습니다. 거꾸로 말해서, 이 문자열만 알면 \(C\)를 알아낼 수 있고 보안이 뚫려버리기 때문에 비밀번호를 다루듯이 다루어야 합니다. HMAC 키 알려달라고요? 네X버 비밀번호 알려달란다고 알려주는 사람 보신 적 있나요?

HMAC 보안은 honeyhouse.save에만 적용되어 있습니다. settings.txt는 딱히 변조를 막을 이유가 없기 때문에 그대로 놔뒀습니다.

첫 화면

개발 막바지에 가장 고역이었던 게 첫 화면과 튜토리얼이었습니다. 개인적으로 Behind Zeroné에서 언급한 것과 같이 "튜토리얼은 설명을 위해 게임의 로직을 어느 정도 침범해야 하기 때문에" 넣기 어렵다고 느끼고 있습니다. 이 게임에서는 로직 침범이라기보다는 여러 가지 이유로 귀찮았는데...

• 구현했던 걸 작은 크기로 다시 구현하는 경우가 많다.
• 테스트를 위해 세이브 파일을 자꾸 지워야 했다.
  • 허니하우스는 세이브 파일이 없을 때만 첫 실행으로 판단하고 조작법과 튜토리얼을 표시합니다.
• 셰이더를 쓸 줄 모른다. 물결 모양으로 사라지는 효과 하나 넣자고 서피스와 블렌드 모드를 남용했다.
• 무엇보다도 육각형 방향이 메인 게임과 다르다.
  • 이거 하나 때문에 첫 화면에 들어가는 모든 리소스를 다시 그려야 했습니다. 😱
  • 그나마 튜토리얼에서는 있는 걸 재활용할 수 있었습니다.

게임 규칙이 워낙 직관적이기 때문에 튜토리얼은 조작법 1페이지 + 규칙 1페이지로 끝냈습니다. 그나마 다행이네요.

결론

드디어 기억나는 내용을 전부 썼네요!

제가 원래 성격이 그렇긴 하지만 이번 게임잼에서도 언제까지 뭘 구현할지와 같은 일정/목표를 전혀 안 잡고 시작했는데, 의외로 막판에 쫓기지 않고 끝냈습니다. 매일 밤마다 어딘가 한 부분씩 묵묵히 작업하다 보니 그렇게 된 건가 하는 생각도 잠깐 했는데, 저번 게임잼도 역시 그렇게 작업했던 걸 생각하면 그냥 기한이 길고 기획이 작아서 그런 것 같습니다. 프로토 게임잼에 몇 번 참여하면서 얻은 귀중한 교훈입니다. 기획은 작게 잡으세요!!!!!

만약에 겜스1로 똑같은 기간 동안 허니하우스를 똑같이 만들라고 한다면... 아마 저는 못 할 것 같습니다. 아까도 얘기했지만 변수 여러 개랑 씨름하는 건 너무 어렵고, 그렇다고 GML 자료구조를 쓰기에는 너무 더럽습니다. 게다가 함수를 못 쓰니 버튼 관리 시스템 같은 걸 만들 수도 없습니다! 구조체와 함수를 필요한 자리에 편하게 만들 수 있고 메모리 관리를 알아서 해주는 엔진의 소중함을 새삼스럽게 깨닫는 기회가 되었네요.

이번 글은 이 정도로 마칠까 합니다. 재밌게 읽으셨길 바라요 🙇‍♂️

1. 2×2 행렬 \(\begin{pmatrix} a & b \\ c & d \end{pmatrix}\)의 역행렬은 \(\frac{1}{ad - bc} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}\)임이 알려져 있습니다. 3×3 행렬은... 주석으로 쓰기에는 복잡하니 적지 않고 위키백과 링크로 대체하겠습니다. ↩

2. 도널드 크누스는 자신의 저서인 The Art of Computer Programming에서 "지나치게 이른 최적화가 만악의 근원"(premature optimization is the root of all evil)이라고 한 바가 있습니다. 사실은 애초에 저걸 어떻게 최적화할지도 잘 모르겠고요. ↩

3. HSV 색 공간에서는 V가 0이면 H와 S에 상관없이 검은색으로 완전히 결정되기 때문에 S 값을 따로 적지 않았습니다. ↩

4. WCAG(Web Content Accessibility Guidelines, 웹 콘텐츠 접근성 가이드라인)은 웹 개발자가 웹 페이지의 접근성을 향상할 수 있도록 기준을 정한 W3C의 표준 문서입니다. 이 문서에서는 텍스트나 UI 요소 등의 색상 대비가 주변 색과 비교해 충분한지를 평가 기준 중 하나로 삼고 있습니다. ↩