잇창명 개발 블로그

LIS 알고리즘은 왜 그렇게 헷갈리는 걸까?

• 수정 • 댓글 달기 문제해결 알고리즘 인터랙티브

가장 긴 증가하는 부분 수열(longest increasing subsequence; LIS)은 어떤 수열이 주어질 때 그 수열의 증가하는 부분 수열(연속하지 않아도 됩니다) 중 가장 긴 것을 찾는 문제입니다. 이 문제를 푸는 여러 가지 알고리즘이 알려져 있지만 문제풀이에서 자주 사용하는 것은 \(O(n \log n)\)입니다.

최근에 트위터에서 지인분이 이 \(O(n \log n)\) 알고리즘에 대해 얘기한 걸 봤는데, 허락을 받아1 내용을 옮기면 다음과 같습니다.

이분탐색으로 LIS를 O(nlogn)에 푸는 풀이에서 몇년째 이해 안되는 부분:
- "이분탐색을 이용하여 LIS를 유지하기 위한 최적의 위치에다가 수를 삽입하는 방식"이라는데 그러면 대체 이 배열은 뭘 의미하나
이게 LIS를 만드는 것도 아닌데

마침 저도 이 알고리즘을 처음 배우면서 비슷하게 의아했던 점이 생각났기 때문에 블로그 글로 올려보려고 합니다.

이 알고리즘이 밟는 단계는 다음과 같습니다.

아무래도 과정이 다소 뜬금없이 느껴지는데, 구글링을 해봐도 읽기 쉽고 속 시원한 답을 제시해주지는 않습니다.

어려운 설명

영문판 위키백과의 설명을 옮기면 \(M\)은 다음을 만족하는 배열입니다. 여기서는 수열을 \(a_i\) 대신 \(X[i]\)로 표기하고 있습니다.

그러면 \(X[i]\)를 처리한 뒤에는 … \(M[j]\)[는] \(K ≤ i\)의 범위에서 길이가 \(j\)이고 \(X[k]\)에서 끝나는 증가하는 부분수열이 존재하도록 하는 가장 작은 값 \(X[k]\)의 인덱스 \(k\)를 저장한다. (문장을 명확하게 다듬어야 함)

Then, after processing \(X[i]\), … \(M[j]\) — stores the index \(k\) of the smallest value \(X[k]\) such that there is an increasing subsequence of length \(j\) ending at \(X[k]\) on the range \(k ≤ i\) (Need to make this statement clearer).

이 설명을 바탕으로 이 알고리즘을 이해해보려고 한다면 다음과 같습니다.

수열의 어떤 원소 \(x\)를 처리하고 있다고 해 봅시다. 이때 배열 \(M\)을 \(a_{M[i]} < x\)인 부분과 \(a_{M[i]} \ge x\)인 부분으로 나눌 수 있습니다.

그러므로 \(x\)가 들어갈 곳은 \(a_{M[i]} \ge x\)를 만족하는 첫 위치 하나뿐이 됩니다. \(a_{M[i]} \ge x\)으로부터 \(\min \left( a_{M[i]}, x \right) = x\)인 것을 생각하면...

아니다, 지금까지 했던 설명은 그냥 잊어주세요. 헷갈리는 문장 때문에 글이 어려워지고 있네요. 당연히 이 얘기를 하려고 한 건 아니고, 쉬운 설명을 생각했으니 들어주세요.

조금 더 쉬운 설명

LIS를 구성하는 과정을 트리로 만든다면 어떻게 될까요?

바로 위의 이 애니메이션은 인터랙티브입니다! 원하는 수열을 공백이나 콤마로 구분해서 입력하고 적용을 눌러보세요. 버튼이나 슬라이더를 이용해 재생해볼 수 있습니다. 공간상의 문제로 -999 이상 9999 이하의 정수만 지원합니다.

DP 알고리즘 설명을 보면 부분 문제를 \(x\)번째 원소로 끝나는 부분 수열로 잡는 경우를 종종 볼 수 있고, 이 경우에는 보통 기존의 부분 문제의 맨 끝에 \(x\)번째 원소를 하나 더 붙이거나 여의치 않으면 \(x\)번째 원소만 있는 부분 수열이 해가 됩니다.

"맨 끝에 하나 더 붙인다"고 하니 트리로 만들어보기 좋겠네요. 이 방법으로 LIS 트리(급조한 이름입니다)를 만들어 봅시다. 루트는 가상의 "0번째" 원소, 즉 \(-\infty\)고 수열의 각 원소가 자기 자신으로 끝나는 LIS를 이루기 좋은 곳에 자식으로 붙습니다. 모든 원소는 수열에 등장하는 순서대로 처리되므로 순서가 꼬여서 LIS를 이루지 않는 경우는 없습니다.

위 애니메이션에서는 새로운 노드가 차례대로 -inf 노드 아래에 생기고, 적당한 자리를 찾은 뒤 그 위치로 이동하는 모습을 볼 수 있습니다.

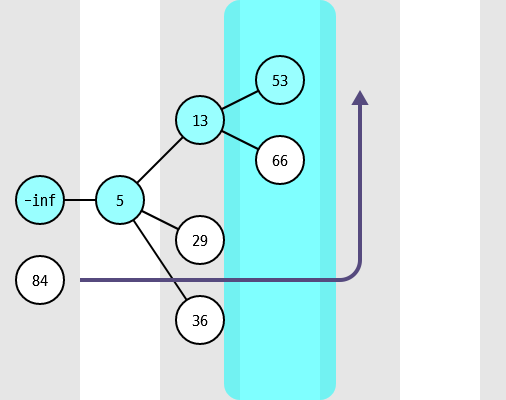
LIS 트리의 어느 한 순간. 루트 노드 밑에 84 노드가 있고 오른쪽 위로 화살표가 뻗어 있다.

LIS의 정의에 의해 모든 자식 노드의 값은 부모 노드보다 크고("부모-자식 성질"이라고 하겠습니다), 루트 노드의 깊이(depth)를 0으로 정의하면 각 노드의 깊이가 그대로 LIS의 길이가 됩니다. 특히 LIS 트리가 완성되면 가장 깊은 노드의 깊이가 문제의 답이 되고, -inf 노드부터 가장 깊은 노드까지의 경로가 가장 긴 LIS 중 하나가 됩니다.

트리를 만드는 규칙

아까 "LIS를 이루기 좋은 곳"이 어딘지 안 말하고 넘어갔는데, LIS 트리의 성질을 보면서 차근차근 생각해 봅시다.

LIS를 최대한 길게 만들려면 가능한 한 가장 깊은 노드를 찾아 자식으로 붙는 것이 제일 좋겠죠. 그런데 어떤 하나의 깊이에서 모든 노드의 값이 너무 커서 자식으로 붙을 수 없는 경우를 생각해볼 수 있습니다. 가장 작은 노드에 붙을 수 없으면 그것보다 더 큰 노드에도 당연히 붙을 수 없으니 깊이별로 최솟값 노드를 기록해 둡시다. 새로 붙일 노드와 최솟값을 비교해서 전자가 후자 이하면 그 깊이는 볼 필요도 없이 넘어가면 되겠네요.

위 애니메이션에서 아래 이미지와 같이 하늘색으로 색칠한 것이 최솟값 노드이고, 노드가 하나라도 있는 세로줄마다 하나씩 있습니다. 잘 보면 최솟값 노드의 값은 같은 세로줄의 다른 노드보다 작거나 같다는 것을 확인할 수 있습니다.

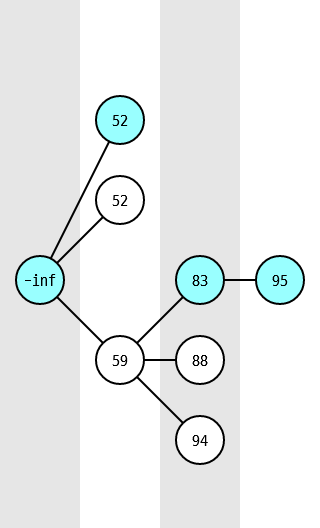
LIS 트리에서 노드 -∞, 52, 83, 95가 하늘색으로 색칠되어 있다.

노드가 너무 큰 경우를 제외하고 난 뒤에는 남은 노드 중에 붙을 만한 것을 찾아야 되는데, 이때도 아까 기록해 둔 최솟값 노드를 요긴하게 쓸 수 있습니다. 위 문단에서 자식으로 붙일 만한 노드가 있는지를 최솟값 노드로 판정했으니 이 판정을 통과했다면 최솟값 노드에는 반드시 붙일 수 있음을 알 수 있습니다.

위의 두 문단에서 얘기한 것을 종합하면 새로운 노드는...

  1. 현재 트리의 모든 깊이 중에
  2. 최솟값 노드가 자신보다 작은 것만 남긴 뒤 (부모-자식 성질을 만족시키기 의해)
  3. 남은 것 중 가장 깊은 깊이의 (LIS의 길이를 최대화하기 위해)
  4. 최솟값 노드 (여기에는 붙일 수 있음이 보장되므로)

에 자식으로 붙는다는 규칙을 만들어볼 수 있습니다. 이 규칙을 염두에 두면서 애니메이션을 다시 재생해보고 오는 것도 좋겠습니다.

LIS 트리에서 발견한 LIS 알고리즘

규칙을 만들었으니 이제 2~3번 과정을 최적화해볼 수 있습니다. 부모-자식 성질을 적용해보면 깊이 \(x-1\)의 최솟값이 \(m\)이면 깊이 \(x\)의 최솟값은 \(m\)보다 커야 한다는 것을 알 수 있습니다. 즉, 최솟값 노드의 배열은 증가수열이고 오름차순 정렬되어 있습니다. 이 성질이 없었다면 배열의 가장 깊은 곳부터 하나씩 확인할 수밖에 없는데, 이제는 정렬되어 있다는 것을 알고 있으니 이분 탐색을 쓸 수 있겠네요. "가상의 0번 원소"(aka \(-\infty\))는 어차피 무엇과 비교해도 더 작으니 이분 탐색에서 제외해도 되겠습니다.

이쯤에서 LIS 트리를 만드는 규칙을 다시 한 번 살펴봅시다.

  1. 현재 트리의 모든 깊이 중에
  2. 최솟값 노드가 자신보다 작은 것만 남긴 뒤 (부모-자식 성질을 만족시키기 의해)
  3. 남은 것 중 가장 깊은 깊이의 (LIS의 길이를 최대화하기 위해)
  4. 최솟값 노드 (여기에는 붙일 수 있음이 보장되므로)

이 규칙만 따르면 최솟값이 아닌 노드는 확인할 필요가 없습니다. 나머지 다른 노드를 치우면 최솟값 노드의 배열만 남는데, 뭔가 익숙하게 느껴진다면 바로 맨 처음에 언급한 문제의 배열 \(M\)입니다.

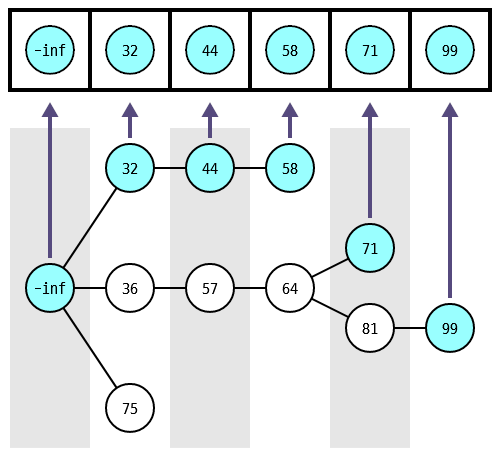
LIS 트리에서 하늘색으로 색칠된 노드를 위의 배열에 옮겨 담은 모습.

규칙을 \(M\) 위주로 다시 써 볼까요?

  1. 현재 트리의 모든 깊이 중에
  2. 최솟값 노드가 자신보다 작은 것만 남긴 뒤 배열 \(M\) 전체에서
  3. 남은 것 중 가장 깊은 깊이의 자신보다 작은 마지막 원소를 이분 탐색으로 찾은 뒤
  4. 최솟값 노드 그 다음 위치에 업데이트 (다음 위치가 없으면 맨 끝에 삽입)

여기서 3~4번 과정을 더 줄일 수 있습니다.

  1. 배열 \(M\) 전체에서
  2. 자신 이상인 첫 원소를 이분 탐색으로 찾아서 (즉, std::lower_bound)
  3. 업데이트 (없으면 맨 끝에 삽입)

글의 맨 위에서 봤던 \(O(n \log n)\) LIS 알고리즘을 재발견했네요!

지금까지 했던 "조금 더 쉬운 설명"과 위키백과에서 했던 "어려운 설명"을 비교해보면 사실 같은 것을 말하고 있음을 알 수 있습니다. 헷갈리는 문장으로 썼던 해설을 다시 한번 읽어봅시다.

수열의 어떤 원소 \(x\)를 처리하고 있다고 해 봅시다. 이때 배열 \(M\)을 \(a_{M[i]} < x\)인 부분과 \(a_{M[i]} \ge x\)인 부분으로 나눌 수 있습니다.

  • 전자의 경우 \(M[i]\)를 덮어쓰려고 하면 \(a_{M[i]} < x\)이므로 \(M\)의 "가장 작은 값" 조건이 깨집니다.

알고 보면 이 부분은 LIS 트리를 만드는 규칙 중 "3. 남은 것 중 가장 깊은 깊이의"와 같고...

  • 후자의 경우 \(a_{M[i]}\)로 끝나는 부분수열 \(b\)에 대해(위 조건에 대해 존재가 보장됩니다) \(b\)의 맨 끝에 \(x\)를 삽입하려고 하면(즉, \(M[i + 1]\)을 덮어쓰려고 하면) \(a_{M[i]} \ge x\)이므로 LIS 상태가 깨집니다.

이 부분은 "2. 최솟값 노드가 자신보다 작은 것만 남긴 뒤"와 같습니다. 솔직히 아직도 헷갈리네요.

개인적으로 위키백과의 설명이 어렵게 느껴졌던 이유는 배열 \(M\)이 LIS 트리에서 따라오는 개념인데도 LIS 트리를 전혀 언급하지 않고 \(M\)만 설명하려고 했기 때문이라고 생각하고 있습니다. 말하자면 배열 \(M\)은 LIS 트리의 그림자인 셈이죠.

응용: 백준에서 문제 풀어보기

LIS 트리를 이해했다면 백준의 14003번 "가장 긴 증가하는 부분 수열 5" 같은 문제에도 응용할 수 있습니다.

LIS 트리의 모든 노드는 ("가상의 0번 원소"를 제외하고) 부모가 정확히 하나씩이니 \(M\) 이외에 각 노드의 부모를 기록하는 \(O(n)\)짜리 배열을 하나 만들고 이 두 배열로 LIS 트리를 만듭니다. 모든 \(A_i\)를 읽은 뒤에는 \(M\)의 가장 끝에서 부모 배열을 타고 내려가면 LIS를 복구할 수 있습니다.

# 복붙을 방지하기 위해 Python과 비슷한 의사코드로 작성합니다.
# 자신 있는 언어로 옮겨 적으면서 글을 잘 이해했는지 확인해 주세요.

N = input()
A = []
for i in [0, N):
	A[i] = input()
M = [-1] # 인덱스를 저장합니다. -1은 가상의 0번째 원소입니다.
parent = [] # 부모의 인덱스를 저장합니다.

for i in [0, N):
	m_index = 1 + M[1:] # 첫 원소를 제외하고
		.map(x => A[x]) # 인덱스를 실제 값으로 바꾼 뒤
		.lower_bound(A[i]) # 이분 탐색. 자리가 없으면 맨 끝에서 한 칸 뒤의 인덱스
	parent[i] = M[m_index - 1]
	M[m_index] = i

LIS = [M[-1]] # M의 마지막 원소
for i in [1, ∞):
	next = parent[LIS[i - 1]] # LIS 트리를 타고 내려갑니다.
	if next == -1:
		break
	LIS[i] = next

print(LIS.length() + "\n")
for x in LIS.reverse(): # 맨 끝의 원소부터 나오므로 뒤집습니다.
	print(x + " ")

아마 앞으로도 가끔씩 문제풀이 알고리즘을 다루는 글을 올릴 것 같습니다. 조금이라도 쉽게 이해할 수 있도록 제가 글을 잘 썼으면 하는데 아무래도 쉽지는 않네요. 앞으로도 잘 부탁드립니다 🙇‍♂️

  1. 해당 계정은 트윗을 비공개로 설정하고 있습니다. ↩

LIS 알고리즘은 왜 그렇게 헷갈리는 걸까?