현재 블로그 이전 작업 중입니다. 빠른 시일 내에 새 블로그로 글을 이전하도록 하겠습니다.
이 글은 메이플스토리의 스타포스 시스템이 아닌, solved.ac의 만우절 이벤트에 대한 글입니다.
2017년에 solved.ac 개발자 shiftpsh님의 블로그에 올라왔던 모든 캐릭터를 모으기 위해서는 얼마를 써야 하는가 글을 재밌게 읽었던 기억이 있습니다. 제목 그대로 게임에서 뽑기를 해서 모든 캐릭터를 모으는 비용의 기댓값을 구하는 글인데, 5년 뒤에 solved.ac 만우절 이벤트로 확률 이벤트가 열리는 걸 보니 신기하네요. 이 글은 이벤트가 열려 있는 4월 1일에 쓰기 시작했는데 지금은 제가 글을 너무 느리게 써서 마감됐습니다.
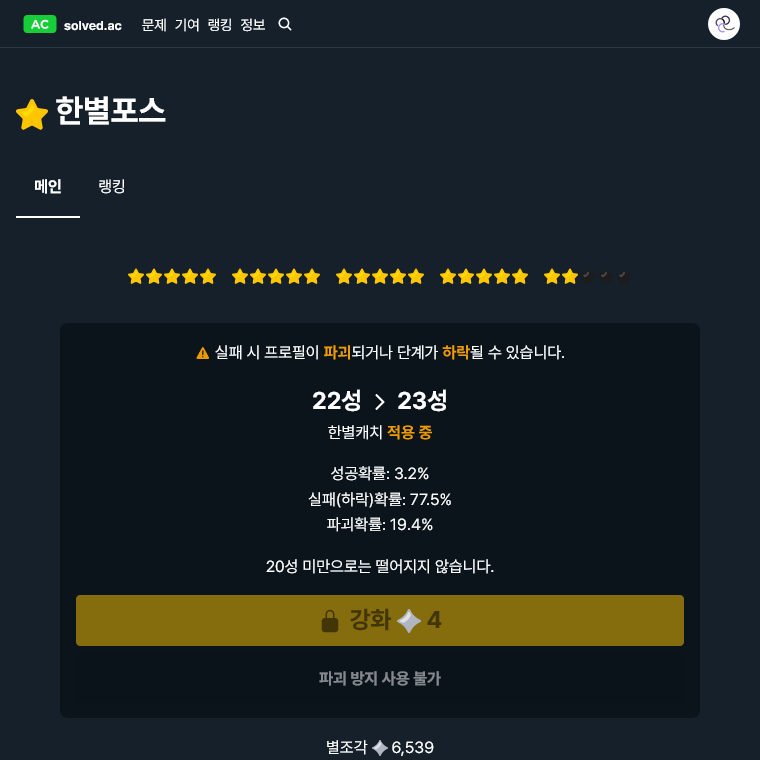
무슨 이벤트였을까?
이번에 이벤트로 열렸던 한별포스는 메이플스토리(제가 메이플스토리를 한 적이 없어서 설명이 틀릴 수 있는 점 감안해주세요)의 스타포스 시스템처럼 프로필을 강화하는 시스템입니다. 당연히 만우절이기 때문에 강화한다고 스탯이 바뀌는 건 아니고 이벤트가 끝날 때 별 개수에 따라 소정의 별조각1을 지급한다고 합니다.
강화 단계는 0성부터 25성까지 있고 별조각을 들여 강화를 시도할 수 있으며, 일정한 확률에 따라 다음 결과 중 하나가 나올 수 있습니다.
- 성공: 강화 단계가 1성 늘어납니다.
- 실패(하락): 강화 단계가 1성 줄어듭니다.
- 실패(유지): 강화 단계가 늘어나지 않습니다.
- 실패했을 때 강화 단계가 어떻게 바뀔지는 강화 시도 이전의 단계에 따라 다릅니다. 10성 → 11성까지와 15성 → 16성, 20성 → 21성("완충 구간")에서는 실패(유지), 이외 단계에서는 실패(하락)만 나옵니다.
- 파괴: 강화 단계가 12성으로 돌아갑니다.
- 12성 → 13성 이상에서만 발생합니다. 실제 메이플스토리에서는 파괴 이후 12성 장비를 복구하는 과정이 추가로 있는 것 같습니다.
이외에도 추가로 다음과 같은 시스템이 있었고 모두 실제 메이플스토리에서 따온 것 같습니다.
- 한별캐치
한별이가 그려진 프로필 배경을 사용하고 있으면 강화 성공 확률이 1.05배가 되고, 실패/파괴 확률이 원래 비율에 비례해 줄어듭니다. 실제 메이플스토리에서는 강화할 때마다 타이밍을 맞춰서 키를 누르는 미니게임으로 구현되어 있다고 합니다. - 파괴 방지 강화
12성 → 13성부터 16성 → 17성까지는 일반 강화보다 별조각을 더 많이 소모하는 대신 파괴 확률이 0%로 확정되는 강화를 할 수 있습니다. 성공 확률은 변하지 않습니다. - CHANCE TIME! (이하 "찬스타임")
강화 결과가 2회 연속 실패(하락)인 경우 무료로 강화 단계를 무조건 1성 올려즙니다. 실패(유지)와 파괴는 계산하지 않는 것으로 기억하고 있습니다.
확률과 비용
강화 단계별 별조각 비용과 성공/실패/파괴 확률을 아래 표에 정리해 두었습니다. 강화 확률은 NEXON NOW에 공개되어 있고, 강화 비용은 제가 기억하는 대로 써넣었는데 shiftpsh님이 회고에서 밝힌 비용과는 차이가 있습니다. 여건이 되면 아래의 확률표를 다시 계산할 예정입니다.
- 확률의 단위는 %, 비용의 단위는 별조각 1개입니다. 확률은 소수점 아래 셋째 자리에서 반올림합니다.
- 강화 단계가 \(n\)인 줄은 \(n\)성에서 \(n+1\)성으로 강화를 시도한다는 의미입니다.
- '성공*', '실패*', '파괴*' 값은 한별캐치가 켜져 있을 때의 확률입니다. 파괴 방지 강화의 확률은 비교적 쉽게 계산할 수 있기 때문에 추가하지 않았습니다.
- 확률 값 앞의 *는 실패 시 판정이 실패(유지)임을 의미합니다.
| 단계 | 비용 | 파괴 방지 비용 | 성공 | 실패 | 파괴 | 성공* | 실패* | 파괴* |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | - | 95 | *5 | - | 99.75 | 0.25 | - |
| 1 | 1 | - | 90 | *10 | - | 94.5 | 5.5 | - |
| 2 | 1 | - | 85 | *15 | - | 89.25 | 10.75 | - |
| 3 | 1 | - | 85 | *15 | - | 89.25 | 10.75 | - |
| 4 | 1 | - | 80 | *20 | - | 84 | 16 | - |
| 5 | 1 | - | 75 | *25 | - | 78.75 | 21.25 | - |
| 6 | 1 | - | 70 | *30 | - | 73.5 | 26.5 | - |
| 7 | 1 | - | 65 | *35 | - | 68.25 | 31.75 | - |
| 8 | 1 | - | 60 | *40 | - | 63 | 37 | - |
| 9 | 1 | - | 55 | *45 | - | 57.75 | 42.25 | - |
| 10 | 2 | - | 50 | *50 | - | 52.5 | 47.5 | - |
| 11 | 2 | - | 45 | 55 | - | 47.25 | 52.75 | - |
| 12 | 2 | 10 | 40 | 59.4 | 0.6 | 42 | 57.42 | 0.58 |
| 13 | 2 | 10 | 35 | 63.7 | 1.3 | 36.75 | 61.99 | 1.27 |
| 14 | 2 | 10 | 30 | 68.6 | 1.4 | 31.5 | 67.13 | 1.37 |
| 15 | 3 | 15 | 30 | *67.9 | 2.1 | 31.5 | 66.44 | 2.06 |
| 16 | 3 | 15 | 30 | 67.9 | 2.1 | 31.5 | 66.44 | 2.06 |
| 17 | 3 | - | 30 | 67.9 | 2.1 | 31.5 | 66.44 | 2.06 |
| 18 | 3 | - | 30 | 67.2 | 2.8 | 31.5 | 65.76 | 2.74 |
| 19 | 3 | - | 30 | 67.2 | 2.8 | 31.5 | 65.76 | 2.74 |
| 20 | 4 | - | 30 | *63 | 7 | 31.5 | 61.65 | 6.85 |
| 21 | 4 | - | 30 | 63 | 7 | 31.5 | 61.65 | 6.85 |
| 22 | 4 | - | 3 | 77.6 | 19.4 | 3.15 | 77.48 | 19.37 |
| 23 | 4 | - | 2 | 68.6 | 29.4 | 2.1 | 68.53 | 29.37 |
| 24 | 4 | - | 1 | 59.4 | 39.6 | 1.05 | 59.37 | 39.58 |
문제 정의하기
이벤트의 규칙과 수치를 정리했으니 구하고 싶은 것을 정의할 차례입니다. 혹시 모르니 shiftpsh님의 글에서처럼 몇 가지 가정을 추가하겠습니다.
- 내 \(n\)성짜리 프로필을 계속 강화할 때, 처음으로 \(m\)성(단, \(n < m\))이 될 때까지 시도 횟수와 소모되는 별조각의 기댓값은 얼마일까?
- 강화 비용은 항상 위의 표를 따릅니다.
- 강화에 필요한 별조각이 부족한 경우는 없습니다.
- 강화는 한 번씩 하고, 다음 강화를 시도하기 전에 결과를 확인합니다.
- 강화 결과 프로필이 \(m\)성이 되면 강화를 멈춥니다.
- 한별캐치를 사용했을 때와 사용하지 않았을 때 위에서 구하는 기댓값은 얼마나 달라질까?
- 파괴 방지 강화를 사용했을 때와 사용하지 않았을 때 위에서 구하는 기댓값은 얼마나 달라질까?
- "파괴 방지 강화를 사용했을 때"의 정확한 의미는 "파괴 방지 강화가 가능한 12성 → 13성부터 16성 → 17성 구간까지 항상 파괴 방지 강화를 하고, 그렇지 않을 경우 항상 일반 강화를 한다"입니다.
그러게요. 써놓고 보니 이걸 어떻게 풀지 막막하네요.
해결 방법 찾기
고등학교와 대학교에서 기본적으로 확률을 다루는 방법을 배우긴 했지만 아직 헷갈리는 게 많습니다. 이 글도 문제를 "표준적으로" 푸는 방법이 아니라 제가 어떻게든 방법을 찾아서 "야매"로 푸는 과정에 집중하려고 합니다.
처음 10성은 단방향
표를 잘 보면 0성 → 1성부터 9성 → 10성까지는 "단방향"으로 강화가 됩니다. 즉, 단계가 올라가기만 하고 내려가지 않으며, 올라간다고 해도 반드시 한 단계씩만 올라갑니다. 게다가 비용도 1로 고정입니다. 이것저것 어려운 가정은 안 해도 되겠네요.
성공과 (아무 일도 생기지 않는) 실패만 있는 시행에서 처음 성공할 때까지 시행하는 횟수의 기댓값은 기하분포로 쉽게 구할 수 있습니다. 1회 시행에서 성공 확률이 \(p\)면 기댓값은 \(\frac{1}{p}\)이네요.
- 비용의 단위는 별조각 1개입니다. 횟수와 비용의 기댓값은 소수점 아래 3자리에서 반올림합니다.
- '횟수*', '비용*'은 한별캐치가 켜져 있을 때의 기댓값입니다.
| 단계 | 횟수 | 비용 | 횟수* | 비용* |
|---|---|---|---|---|
| 0 | 1.05 | 1.05 | 1.00 | 1.00 |
| 1 | 1.11 | 1.11 | 1.06 | 1.06 |
| 2 | 1.18 | 1.18 | 1.12 | 1.12 |
| 3 | 1.18 | 1.18 | 1.12 | 1.12 |
| 4 | 1.25 | 1.25 | 1.19 | 1.19 |
| 5 | 1.33 | 1.33 | 1.27 | 1.27 |
| 6 | 1.43 | 1.43 | 1.36 | 1.36 |
| 7 | 1.54 | 1.54 | 1.47 | 1.47 |
| 8 | 1.67 | 1.67 | 1.59 | 1.59 |
| 9 | 1.82 | 1.82 | 1.73 | 1.73 |
나머지 15성은 양방향
그런데 11성 → 12성부터는 실패(하락)의 가능성이 있습니다. 즉, 11성에서 10성으로 떨어질 수 있고 계산할 때 이걸 고려해야 합니다. 이외에도 12성 → 13성부터는 파괴 확률이 있고 심지어는 CHANCE TIME!까지 전부 고려해야 합니다. 꺄악!
일단 강화 방식을 보아 마르코프 체인을 사용하는 게 좋을 것 같습니다. 제가 제대로 이해한 게 맞다면, 여러 상태가 있고 각 상태마다 다른 상태로 전이하는 확률이 정해져 있을 때, \(n\)번째 전이 이후에 무슨 상태로 전이했는지의 확률변수를 수열로 늘어놓은 것을 마르코프 체인이라고 합니다.
제가 한 문장으로 요약한다고 좀 복잡하게 쓰긴 했는데, 핵심은 다음 상태로 전이할 확률이 현재 상태에 따라서만 결정된다는 것입니다("마르코프 성질"이라고 합니다). 예를 들어 9성 프로필을 한별캐치 없이 강화했을 때는 이전에 강화 단계가 뭐였는지에 상관없이 55%의 확률로 10성 프로필, 45%의 확률로 9성 프로필이 됩니다. 10성부터는 찬스타임으로 인해 마르코프 성질을 위반하는 것처럼 보이는데, 이전에 실패한 횟수까지 상태로 묶어놓아서 해결할 수 있습니다(예를 들면 직전 강화에서 1번 하락한 13성 프로필).
앞으로 마르코프 체인 상태를 자주 언급할 것 같으니 기호를 몇 개 정의하겠습니다. 아래 모든 기호에서 \(i \in \{0, 1, 2, \cdots, 25\}\)와 \(j \in \{0, 1, 2\}\)를 만족합니다.
- \(H_{ij}\)는 한별캐치가 꺼져 있는 일반 강화의 확률표를 따르는
직전 강화에서 j번 하락한 i성 프로필을 의미합니다. - 한별캐치와 파괴 방지 강화는 별표나 칼표 같은 것을 넣어서 지칭하려고 했는데 글을 다 쓰고 보니 쓸 일이 없어서 지웠습니다.
\(H\)는 Hanbyeolforce에서 따왔습니다. 특히 \(j = 2\)일 때는 찬스타임이 발동된 상태가 됩니다.
삽질의 시간
그런데 솔직히 제가 마르코프 체인을 들어만 봤지 실제로 써본 적이 없습니다. 위에서 정의한 상태로 마르코프 체인을 구성하고 나서 어떻게 할지를 한참 고민했고 제 머릿속에 스쳐지나간 생각 일부를 적어봅니다. 하나 빼고 귀찮아서 실행으로 옮기지는 않았습니다.
- 전이를 무한 번 하고 나면 확률이 어떻게 수렴하지?
- 강화 실패는 어떡하지? 제대로 신경 안 쓰면 기댓값이 과대평가될 것 같은데
- \(i < m\)인 상태를 전부 치우고 그 안에서만 계산할까?
- \(x\)번 강화해서 \(H_{i0}\)이 될 확률을 구해서 전부 합하면?
- 그러면 별조각 개수를 수식에 못 넣는데
- 별조각 개수만큼 중간 상태를 넣어???
- 그러면 실제 메이플 코스트로 계산할 때 계산량 감당을 못하는데
- 별조각 개수만큼 중간 상태를 넣어???
- 그러면 별조각 개수를 수식에 못 넣는데
- \(x\)번 강화해서 \(H_{i0}\)이 될 확률을 구해서 전부 합하면?
- 그냥 나중에 구글 검색해야지
- 이건 실제로 실행에 옮겼습니다.
처음부터 구글링 할걸
결국 구글에 markov chain expected number of steps를 검색했고 수학 스택 익스체인지에서 이런 답변을 읽었습니다. 질문답변 내용을 요약하자면 이렇습니다.
- 질문: 상태 전이 행렬2이 \(\begin{pmatrix} 1 & 0 & 0 \\ 1/2 & 1/4 & 1/4 \\ 1/2 & 1/4 & 1/4 \end{pmatrix}\)인데 상태 3에서 1로 가는 평균 단계 수는 어떻게 계산하나요?
- 답변: \(h(k)\)를 상태 \(k\)에서 1로 가는 단계 수의 기댓값이라고 하면
- \(h(1) = 0\)
- 각 상태로 전이할 확률과 다음 상태의 \(h(k)\)를 고려해서 다른 \(k\)에 대한 \(h(k)\)의 식을 세우고 방정식 풀듯이 풀면 된다.
- 예를 들어 \(h(2) = 1 + \frac{1}{2}h(1) + \frac{1}{4}h(2) + \frac{1}{4}h(3)\)
저는 이 답변을 이렇게 이해했습니다. 모든 상태의 집합 \(S\), 상태 전이 행렬은 \(P\), 멈추고자 하는 상태의 집합 \(S_s\)에 대해
- \(h(x) = 0\) (if \(x \in S_s\); 멈추려는 상태에 이미 도착했으므로)
- \(h(x) = 1 + \sum_{i \in S} P_{xi}h(i)\) (otherwise; 다른 상태로 가는 단계 수 1과 다음 상태에서 \(h\)의 기댓값의 합)
\(x\)성 이상으로 강화하려면 일단 \(H_{x0}\)을 거쳐야 하므로 \(S_s\)에 이것저것 많이 넣을 필요는 없을 것 같습니다. 단계 수 대신 별조각 수의 기댓값을 구하려면 1 대신 별조각 표에서 값을 끌어오면 되겠네요!
진짜로 마르코프 체인 그리기
그런데 아직도 마르코프 체인을 안 만들어놨네요. 빨리 만들고 오겠습니다.
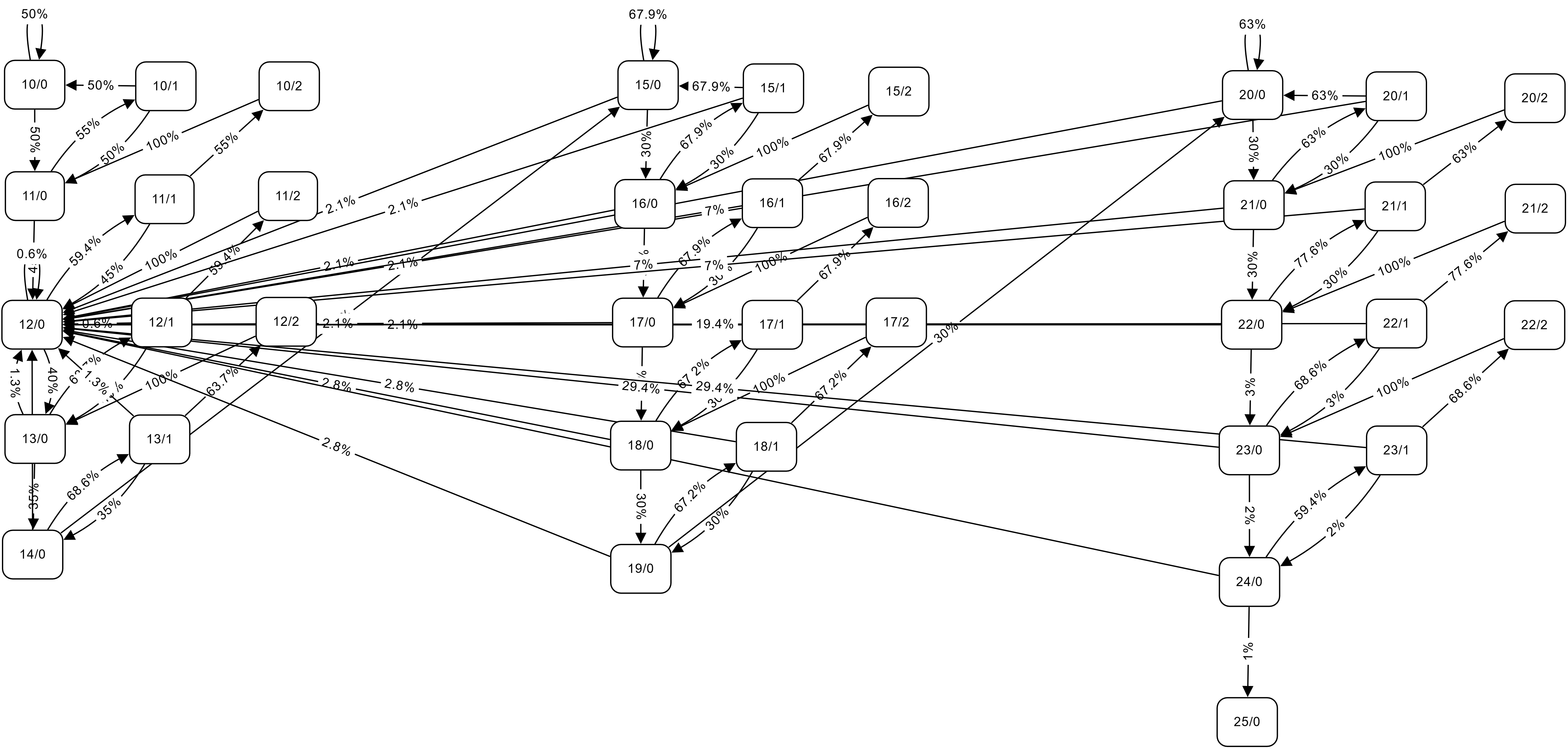
그리드에 맞추는 기능이 없는 에디터에서 만들어서 찍었기 때문에 상태 배치가 좀 삐뚤게 보일 수 있습니다. 견뎌주세요. 길게 누르거나 우클릭을 해서 큰 크기의 원본을 볼 수 있습니다.
위 이미지에는 10성부터 25성까지 가능한 모든 상태와 상태 전이를 그려 두었습니다. 잘 보면 몇 가지 필요 없는 상태는 보이지 않는 것을 알 수 있습니다.
- 일단 10성을 달성하면 9성 이하로 돌아갈 수 없고 9성 이하의 기댓값은 이미 위에 정리해 두었기 때문에 9성 이하의 상태는 생략했습니다.
- 완충 구간으로 인해 도달할 수 없는 일부 상태(예를 들어 \(H_{14,1}\)은 15성에서 강화가 실패(하락)할 수 없으므로 도달할 수 없습니다.)를 생략했습니다.
- 25성에 도달하면 더 이상 강화할 이유가 없으므로 \(H_{25,0}\)의 상태 전이 화살표도 생략했습니다.
그런데 그림을 더 잘 보면 굳이 필요할까 싶은 상태가 3개 더 있습니다. 예를 들어 \(H_{10,1}\)은 \(H_{10,0}\)과 상태 전이가 완전히 같은데 그렇다고 \(H_{10,2}\)로 갈 수 있는 것도 아니니 딱히 \(H_{10,1}\)과 구분할 이유가 없습니다. 이렇게 "구분할 수 없는" 상태 몇 개를 더 합치면 아래 그림과 같아집니다.
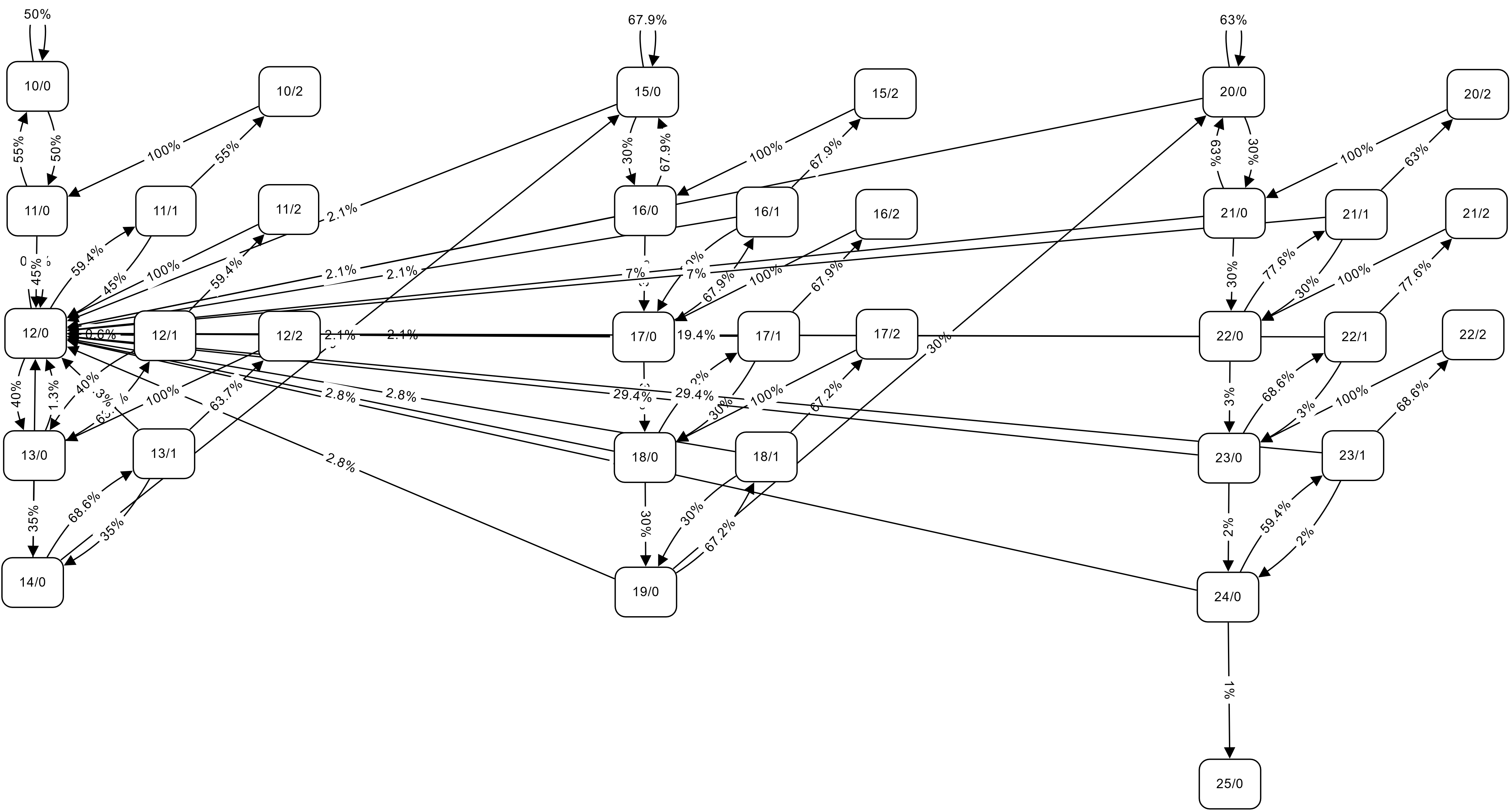
이제 이 그림이랑 위의 그림 사이에 위치가 살짝 틀어진 것도 신경쓰이겠네요. 견뎌주세요. 감사합니다.
편의상 이렇게 남은 모든 상태에 번호를 붙이겠습니다. \(H_{10,0}\)이 1번이고 \(i\) 오름차순, \(j\) 오름차순으로 다음 번호를 붙입니다. 이렇게 붙인 순서대로 나열하면 1번이 \(H_{10,0}\), 2번이 \(H_{10,2}\), 3번이 \(H_{11,0}\), ..., 마지막으로 34번이 \(H_{25,0}\)입니다.
작년에 왔던 선형대수학 죽지도 않고 또 왔네
Honeyhouse를 만들 때 애용했던 행렬을 또 써보려고 합니다. 그러고 보니까 이 글을 올린 게 작년 이맘때쯤이네요.
한별포스 마르코프 체인은 너무 크니 위에서 질문으로 나왔던 상태 3개짜리 마르코프 체인으로 예시를 들어 봅시다. 상태 전이 행렬을 옮겨 적으면 다음과 같습니다.
\[P = \begin{pmatrix} 1 & 0 & 0 \\ 1/2 & 1/4 & 1/4 \\ 1/2 & 1/4 & 1/4 \end{pmatrix}\]또 위 답변대로 연립방정식을 완성한 뒤 이항하면 이렇습니다.
- \(h(1) = 0\)
- \(1h(1) + 0h(2) + 0h(3) = 0\)
- \(h(2) = 1 + \frac{1}{2}h(1) + \frac{1}{4}h(2) + \frac{1}{4}h(3)\)
- \(\frac{1}{2}h(1) - \frac{3}{4}h(2) + \frac{1}{4}h(3) = -1\)
- \(h(3) = 1 + \frac{1}{2}h(1) + \frac{1}{4}h(2) + \frac{1}{4}h(3)\)
- \(\frac{1}{2}h(1) + \frac{1}{4}h(2) - \frac{3}{4}h(3) = -1\)
저번 글에서는 좌표계를 정의하고 조작하는 데 행렬을 쓴다고 했었는데, 사실 행렬로 일차 연립방정식도 풀 수 있습니다! 다음과 같이 식을 구성하고 해를 구하면 벡터 \(\vec{x}\)가 연립방정식의 \(h(1)\), \(h(2)\), \(h(3)\)와 대응합니다.
\[\begin{pmatrix} 1 & 0 & 0 \\ 1/2 & -3/4 & 1/4 \\ 1/2 & 1/4 & -3/4 \end{pmatrix} \vec{x} = \begin{pmatrix} 0 \\ -1 \\ -1 \end{pmatrix}\]좌변은 \(P-I\)의 1번째 행을 \(I\)의 1번째 행으로 바꾼 것이고, 우변은 1번째 행만 빼고 전부 \(-1\)이네요. 내심 이것보다 조금 더 깔끔한 관계를 기대했는데 아쉽습니다. 아무튼 작은 마르코프 체인에서 관찰한 것을 일반화하면, 상태 전이 행렬이 \(P\), 전이하는 비용의 벡터가 \(\vec{v}\)인 마르코프 체인에서, 임의의 상태에서 \(s\)번 상태로 가는 기댓값은 다음 식으로 구할 수 있습니다.
\[(P - I)_{(I,s)}\vec{x} = -\vec{v}_{(0,s)}\]단, \(M_{(N,x)}\)는 행렬 \(M\)의 \(x\)번째 행을 행렬 \(N\)의 \(x\)번째 행으로 바꾸는 연산입니다. 자꾸 기호를 정의하고 싶지 않은데 어쩔 수 없네요. 다른 기호가 있는데 제가 모르고 있는 거라면 알려주세요. 마지막으로 양변의 왼쪽에 역행렬을 곱하면 \(\vec{x}\)에 대한 깔끔한 식을 완성할 수 있습니다.
\[\vec{x} = -(P - I)_{(I,s)}^{-1} \vec{v}_{(0,s)}\]아니면 첨가행렬을 만들어서 RREF를 구해도 됩니다. 나중에 다시 얘기하겠지만 저는 행렬 연산을 직접 구현해야 되는 상황이라서 역행렬보다는 구현하기 쉬워 보이는 RREF 쪽을 선택했습니다.
한별캐치가 꺼져 있는 일반 강화 기준으로 상태 전이 행렬 \(P\)는 다음과 같습니다. 34번째 행(\(H_{25,0}\))까지 오면 더 이상 강화할 필요가 없기 때문에 그냥 0으로 채웠습니다.
\(\begin{pmatrix} \frac{1}{2} & 0 & \frac{1}{2} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \frac{11}{20} & 0 & 0 & 0 & 0 & \frac{9}{20} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & \frac{11}{20} & 0 & 0 & 0 & \frac{9}{20} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{297}{500} & 0 & \frac{3}{500} & 0 & 0 & \frac{2}{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{297}{500} & \frac{3}{500} & 0 & 0 & \frac{2}{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{13}{1000} & \frac{637}{1000} & 0 & 0 & 0 & \frac{7}{20} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{13}{1000} & 0 & \frac{637}{1000} & 0 & 0 & \frac{7}{20} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{7}{500} & 0 & 0 & 0 & \frac{343}{500} & 0 & \frac{3}{10} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{21}{1000} & 0 & 0 & 0 & 0 & 0 & \frac{679}{1000} & 0 & \frac{3}{10} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{21}{1000} & 0 & 0 & 0 & 0 & 0 & \frac{679}{1000} & 0 & 0 & 0 & 0 & \frac{3}{10} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{21}{1000} & 0 & 0 & 0 & 0 & 0 & 0 & \frac{679}{1000} & 0 & 0 & 0 & \frac{3}{10} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{21}{1000} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{679}{1000} & 0 & 0 & 0 & 0 & \frac{3}{10} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{21}{1000} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{679}{1000} & 0 & 0 & 0 & \frac{3}{10} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{7}{250} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{84}{125} & 0 & 0 & 0 & \frac{3}{10} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{7}{250} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{84}{125} & 0 & 0 & \frac{3}{10} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{7}{250} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{84}{125} & 0 & \frac{3}{10} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{7}{100} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{63}{100} & 0 & \frac{3}{10} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{7}{100} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{63}{100} & 0 & 0 & 0 & 0 & \frac{3}{10} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{7}{100} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{63}{100} & 0 & 0 & 0 & \frac{3}{10} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{97}{500} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{97}{125} & 0 & 0 & 0 & 0 & \frac{3}{100} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{97}{500} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{97}{125} & 0 & 0 & 0 & \frac{3}{100} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{147}{500} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{343}{500} & 0 & 0 & 0 & \frac{1}{50} & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{147}{500} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{343}{500} & 0 & 0 & \frac{1}{50} & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{99}{250} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{297}{500} & 0 & \frac{1}{100} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix}\)
솔직히 이 시점에서 꽤 후회하고 있습니다.
그런데 어떻게 계산하지?
그냥 저 위의 행렬을 학교 라이선스로 받은 MATLAB에 넣고 돌려도 되겠지만, 한 가지 아쉬운 점은 MATLAB도 부동소수점을 쓰기 때문에 0.1 + 0.2 == 0.3이 성립하지 않는다는 것입니다. 왠진 모르겠지만 정밀도를 잃어버리기는 싫었기 때문에 BigInt 분수를 원소로 가지는 행렬 연산을 지원하는 무언가를 찾아야 했습니다. 제가 찾아본 언어와 라이브러리가 대충 이렇습니다.
- Wolfram|Alpha (34×34 행렬은 계산 안 해줄 것 같아서 제외)
- https://0.30000000000000004.com/ (분수 지원이 있는 언어를 찾기 위해서)
- Haskell (BigInt 분수 지원은 있는 것 같긴 한데 전혀 익숙하지 않아서 제외)
- Mathematica (유료라서 제외)
- Python
- NumPy (BigInt 분수 지원이 없어서 제외)
- SymPy (너어어어어어어어무 느려서 제외. 분수 원소인 18×18 역행렬 하나를 몇 분이 지나도 못 구했습니다.)
- JavaScript
- npm (BigInt 분수를 지원하는 행렬 라이브러리는 못 찾았습니다.)
결국에는 예전에 백준에서 RREF 문제를 풀던 느낌으로 JavaScript 위에 RREF 연산을 직접 구현했고 분수 지원은 직접 짤 수는 있지만 귀찮아서 big-rational에서 훔쳐왔습니다. 구현을 잘 했길 빌어야겠네요.
SymPy 때문에 실행 시간이 너무 오래 걸리면 어쩌지 했는데 다행히 30초 안에 끝났습니다. 초기 버전의 출력은 이렇게 나왔고 이후 글을 쓰면서 계속 수정했습니다.
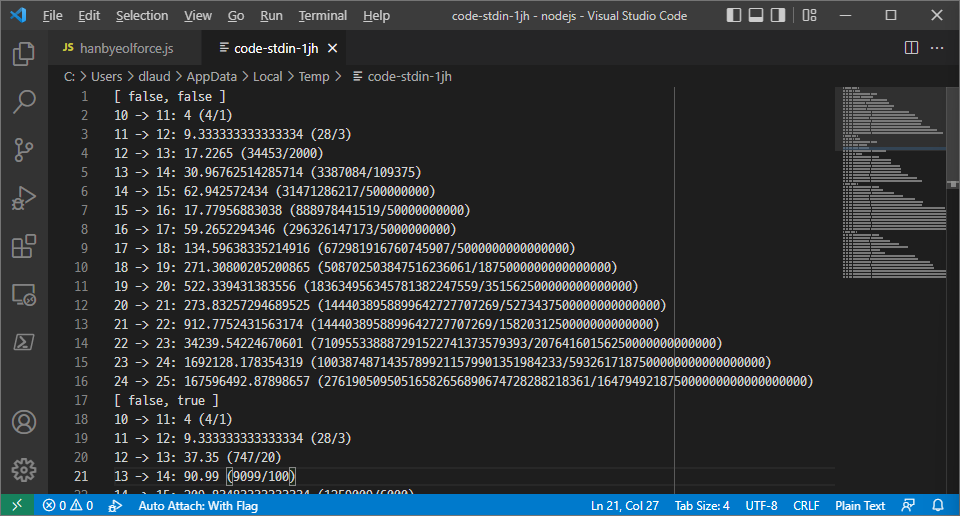
계산 결과로 커다란 분수가 나올 거라는 예상은 했는데 \(\frac{60510970315760784302454536641048593069023488001243566459347392580931999}{611065180773285529890239648437500000000000000000000000000000000}\) 같은 걸 보고 아주조금 후회하긴 했습니다.
표로 정리한 결과
오래 기다리셨습니다. 일단 일반 강화를 사용하는 결과부터 보여드리겠습니다.
- 실패(하락) 횟수가 0인 상태에서 시작한다고 가정합니다.
- 맨 아랫줄의 0 → 25는 중간 과정 없이 0성에서 25성까지 강화하는 기댓값입니다.
- 임의의 \(n\)과 \(m\)(단, \(n < m\))에 대해 \(n\)성에서 \(m\)성으로 강화하는 기댓값은 \(n\) → \(n + 1\)부터 \(m - 1\) → \(m\)까지 전부 합해서 구할 수 있습니다.
| 단계 | 횟수 | 비용 | 횟수* | 비용* |
|---|---|---|---|---|
| 0 | 1.05 | 1.05 | 1.00 | 1.00 |
| 1 | 1.11 | 1.11 | 1.06 | 1.06 |
| 2 | 1.18 | 1.18 | 1.12 | 1.12 |
| 3 | 1.18 | 1.18 | 1.12 | 1.12 |
| 4 | 1.25 | 1.25 | 1.19 | 1.19 |
| 5 | 1.33 | 1.33 | 1.27 | 1.27 |
| 6 | 1.43 | 1.43 | 1.36 | 1.36 |
| 7 | 1.54 | 1.54 | 1.47 | 1.47 |
| 8 | 1.67 | 1.67 | 1.59 | 1.59 |
| 9 | 1.82 | 1.82 | 1.73 | 1.73 |
| 10 | 2.00 | 4.00 | 1.90 | 3.81 |
| 11 | 4.67 | 9.33 | 4.24 | 8.49 |
| 12 | 8.61 | 17.23 | 7.53 | 15.06 |
| 13 | 15.48 | 30.97 | 13.00 | 26.00 |
| 14 | 31.47 | 62.94 | 25.25 | 50.49 |
| 15 | 7.22 | 17.78 | 6.16 | 15.50 |
| 16 | 24.08 | 59.27 | 19.56 | 49.20 |
| 17 | 54.34 | 134.60 | 41.86 | 105.97 |
| 18 | 109.57 | 271.31 | 79.44 | 201.00 |
| 19 | 211.15 | 522.34 | 143.49 | 362.64 |
| 20 | 111.12 | 273.83 | 76.30 | 192.29 |
| 21 | 370.40 | 912.78 | 242.24 | 610.44 |
| 22 | 13920.80 | 34239.54 | 8874.74 | 22301.33 |
| 23 | 688052.14 | 1692128.18 | 418011.91 | 1050236.02 |
| 24 | 68148164.17 | 167596492.88 | 39413962.95 | 99025394.05 |
| 0 → 25 | 68851100.79 | 169325190.52 | 39841523.49 | 100099585.20 |
파괴 방지 강화는 별도 표로 정리했습니다.
| 단계 | 횟수 | 비용 | 횟수* | 비용* |
|---|---|---|---|---|
| 0 | 1.05 | 1.05 | 1.00 | 1.00 |
| 1 | 1.11 | 1.11 | 1.06 | 1.06 |
| 2 | 1.18 | 1.18 | 1.12 | 1.12 |
| 3 | 1.18 | 1.18 | 1.12 | 1.12 |
| 4 | 1.25 | 1.25 | 1.19 | 1.19 |
| 5 | 1.33 | 1.33 | 1.27 | 1.27 |
| 6 | 1.43 | 1.43 | 1.36 | 1.36 |
| 7 | 1.54 | 1.54 | 1.47 | 1.47 |
| 8 | 1.67 | 1.67 | 1.59 | 1.59 |
| 9 | 1.82 | 1.82 | 1.73 | 1.73 |
| 10 | 2.00 | 4.00 | 1.90 | 3.81 |
| 11 | 4.67 | 9.33 | 4.24 | 8.49 |
| 12 | 8.68 | 37.35 | 7.58 | 34.21 |
| 13 | 15.49 | 90.99 | 13.01 | 80.57 |
| 14 | 30.68 | 209.83 | 24.62 | 178.06 |
| 15 | 3.33 | 50.00 | 3.17 | 47.62 |
| 16 | 11.11 | 166.67 | 10.08 | 151.17 |
| 17 | 29.64 | 370.61 | 25.10 | 313.34 |
| 18 | 66.06 | 733.13 | 52.33 | 575.79 |
| 19 | 132.26 | 1383.62 | 98.06 | 1009.44 |
| 20 | 72.69 | 723.18 | 54.05 | 532.47 |
| 21 | 242.31 | 2410.60 | 171.59 | 1690.39 |
| 22 | 9091.89 | 90705.68 | 6273.88 | 62058.12 |
| 23 | 449332.05 | 4483568.83 | 295471.21 | 2923396.36 |
| 24 | 44504019.46 | 444076050.87 | 27859632.04 | 275645195.90 |
| 0 → 25 | 44963075.87 | 448656528.23 | 28161855.77 | 278635288.64 |
특히 한별캐치를 가지고 일반 강화로 0성에서 22성(강화 성공 확률이 2자리 이상인 마지막 단계. 이번 이벤트에서는 상품이 걸려 있는 마지막 단계이기도 했습니다)까지 강화하는 데는 평균 673.88회 강화, 별조각 1653.80개가 필요합니다. 이벤트 기간 내에 23성까지 달성한 분도 있었는데, 이때는 평균 9548.62회 강화, 별조각 23955.13개가 필요합니다. 1등 상품이 별조각 총 13850개인 것을 고려하면 22성까지만 달성하고 멈추는 게 좋네요.
저단계에서는 한별캐치의 효과가 눈에 띄지 않지만(10성 → 11성에서 강화 횟수 ~5%, 별조각 ~4.75% 절약), 고단계로 갈수록 두드러집니다(21성 → 22성에서 강화 횟수 ~34.6%, 별조각 ~33.12% 절약). 파괴 방지 강화를 한다면 강화 횟수는 조금 줄어들지만, 그 대신 소모하는 별조각 수는 급격히 많아집니다(21성 → 22성에서 강화 횟수 ~34.58% 감소, 별조각 ~164.09% 증가).
마지막으로 제가 가장 궁금했던 0성 → 25성 강화는... 음... 솔브드에서 별조각 1억 개를 쓰면서 강화 버튼을 4000만 번 누르고 싶지는 않네요.
마지막으로 이 글을 쓰면서 작성했던 코드를 그냥 버리기는 아까우니 GitHub에 올려 두었습니다. 이 글에 올린 값 이외에 자세한 내용이 궁금하다면 확인해 주세요. 읽어주셔서 감사합니다 🙇♂️