잇창명 개발 블로그

타입을 미분할 수 있다고?

• 수정 • 댓글 달기 TIL 타입이론

뚱딴지같은 소리일 것 같긴 한데 솔직히 저도 놀랐습니다.

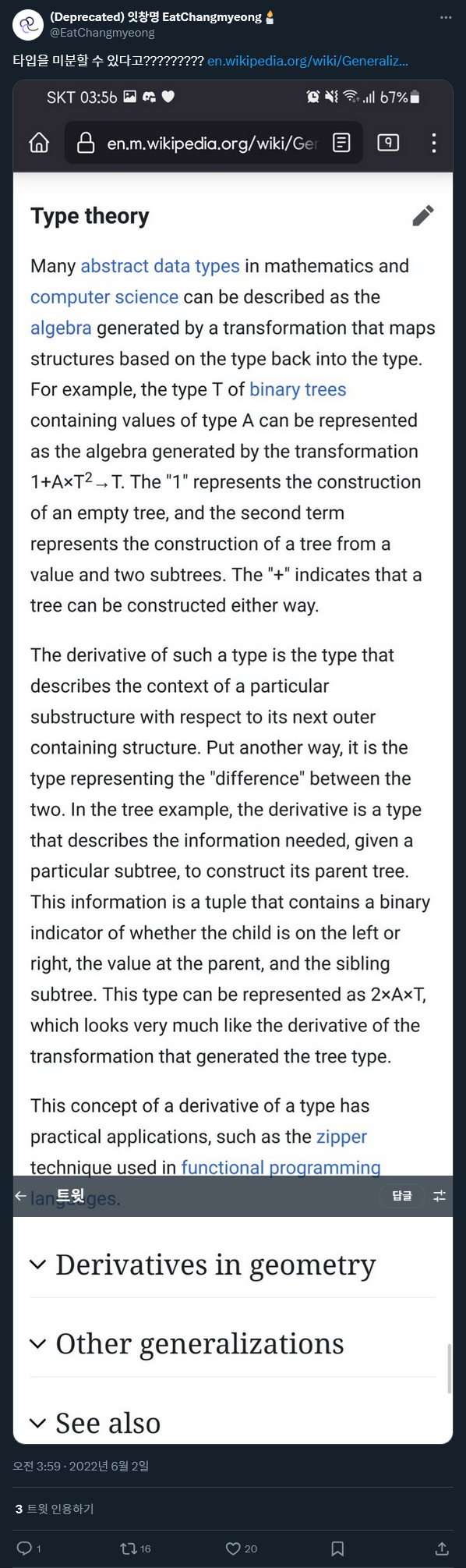
위에 인용한 이미지에서 제가 하고 싶은 말을 다 하고 있긴 한데 그래도 블로그 글로 옮겨보려고 합니다. 안 쓰고 그냥 넘어갔다가 후회하는 것보다는 낫겠죠.

의미를 유지하면 같은 타입

본론으로 들어가기 전에 부연 설명부터 하겠습니다.

이 글에서는 "같은 타입"이라는 표현을 원래 의미와 다르게 사용합니다. 조금 더 자세히 말해보자면, "같은 타입"이란 "그 타입이 가질 수 있는 값이 같음"을 넓게 해석한 것입니다.

C로 예를 들자면, 아래의 Foo와 Bar는 C의 타입 시스템상에서 다른 타입입니다.

typedef int Foo;

typedef struct {
	int value;
} Bar;

Foo x = 1;
Bar y = { 1 };
x = y; // assigning to 'Foo' (aka 'int') from incompatible type 'Bar'

...하지만 Foo에서 Bar로, 또 Bar에서 Foo로 "자연스럽게" 변환하는 함수를 만들어서 두 타입 사이를 자유롭게 오갈 수 있습니다.

Bar foo_to_bar(Foo x) {
	Bar y = { x };
	return y;
}
Foo bar_to_foo(Bar x) {
	return x.value;
}

Foo x = 1;
Bar y = { 1 };
x = bar_to_foo(y);

별도의 언급이 없으면 이렇게 "자연스러운" (값의 의미를 바꾸지 않는) 일대일 대응이 존재하는 타입을 "같다"고 하겠습니다. 예를 들어 int와 unsigned int는 같지 않습니다(unsigned int와 int가 서로 표현하지 못하는 값이 있으므로). 수학 용어로는 동형사상이 존재한다고 하는 것 같습니다.

대수적 자료형

이미지로 올린 위키백과 글을 자세히 읽어 보면 다음과 같은 내용이 있습니다.

… 예를 들어, 타입 A의 값을 담고 있는 이진 트리의 타입 T는 사상 1+A×T² → T로 생성되는 대수로 나타낼 수 있다.

… For example, the type T of binary trees containing values of type A can be represented as the algebra generated by the transformation 1+A×T² → T.

타입을 표현하는데 덧셈이나 곱셈을 동원하는 게 낮설어 보일 것 같습니다. 이런 식으로 표현할 수 있는 타입을 대수적 자료형이라고 합니다. 한국어 위키백과에서는 "다른 자료형의 값을 가지는 자료형"이라고 설명하는데, 개인적으로 이것보다는 타입을 합과 곱으로 나타낼 수 있다는 것이 대수적 자료형의 핵심과 더욱 가깝다고 생각합니다.

합과 곱을 언급했으니 더욱 익숙한 쪽부터 설명해 보겠습니다.

곱 타입

곱 타입을 설명하라고 하면 아마 C의 구조체를 언급하는 게 제일 쉬울 것 같습니다. 여기부터는 나중에 설명의 편의를 위해 대수적 자료형을 지원하는 Rust로 예시를 들어 보겠습니다. 문법이 그렇게까지 다르지는 않으니 걱정하지 말아 주세요.

struct Foo { // = i32×char
	// i32는 32비트 부호 있는 정수형입니다. int와 비슷합니다
	member_one: i32,
	// C의 char와 비슷하지만 1바이트보다 큽니다.
	member_two: char,
}

이게 왜 곱 타입인지 설명하는 데는 역시 원소의 개수를 따지는 게 제일 편할 것 같습니다. 타입 \(A\)의 원소의 개수를 \(\lvert A \rvert\)로 표기할 때, \(\lvert A \times B \rvert = \lvert A \rvert \times \lvert B \rvert\)가 성립합니다(\(\lvert A \rvert\)가 무한인 경우는 이 글에서 생각하지 않겠습니다. 성립한다고만 알아 주세요). 집합론적 관점으로 보면 곱 타입은 곱집합에 해당합니다.

위 식에 \(A\) 대신 i32, \(B\) 대신 char를 넣어서 생각해 보세요. 감이 오시나요?

Rust에서는 대수적 자료형을 자주 사용하다 보니 간단하게 곱 타입을 만들 수 있는 방법으로 튜플 타입을 제공합니다.

// typedef struct { ... } TypeAliasFoo;
type TypeAliasFoo = (i32, char); // = i32×char

// or

// C 스타일 구조체와 비슷한데 원소를 번호로 지칭합니다.
struct TupleStructFoo(i32, char, f64, String); // = i32×char×f64×String

TupleStructFoo에서 볼 수 있듯이 굳이 2개만이 아니라 원하는 개수의 타입을 튜플에 넣을 수 있습니다. 혹시 2개 미만도 되냐고요?

// 1-tuple은 괄호와 혼동을 방지하기 위해
// 끝에 trailing comma를 하나 달아줘야 합니다.
// `(i32,)`와 `(i32)` (aka `i32`)는
// 이 글에서는 "같은" 타입으로 취급하지만
// Rust의 타입 시스템상 다른 타입입니다.
type OneTuple = (i32,); // = i32

type ZeroTuple = (); // ???????

타입 0개의 곱도 있을 수 있습니다. 예를 들어, ZeroTuple은 단 하나의 값 ()만 가질 수 있는 타입입니다.

이런 타입을 단위 타입이라고도 하는데, 곱 타입의 항등원으로 작용합니다(임의의 타입 T에 대해 ()×T = T×() = T). 곱의 항등원이니 여기서부터는 1로 표기하겠습니다(정수 1이 아님에 유의).

합 타입

C에는 합 타입에 대응하는 것이 없고, 그나마 가장 가까운 것으로 공용체가 있습니다. Rust로 합 타입을 만들어 보겠습니다.

enum Foo {
	One,
	Two,
	Three,
	Four,
}

이거 그냥 열거형 아니에요?

네, 열거형 맞긴 합니다. 그런데 잘 보세요.

enum Foo { // = 1 + i32 + char + i32×char
	One,
	Two(i32), // ???????
	Three(char),
	Four(i32, char),
}

열거형에서 무슨 선택지를 골랐느냐에 따라 추가로 값을 저장할 수 있습니다. C에서 비슷한 것을 만들라고 하면 이 정도가 한계인 것 같습니다.

enum FooEnum { One, Two, Three, Four };
union Foo {
	enum FooEnum discriminant;
	struct { enum FooEnum _; } one;
	struct { enum FooEnum _; int value; } two;
	struct { enum FooEnum _; char value; } three;
	struct { enum FooEnum _; int value1; char value2; } four;
};

union Foo에서 올바른 원소를 찾아가는 건 당연히 프로그래머가 직접 해야 합니다. Rust에서는 대참사가 일어나지 않도록 패턴 매칭을 통해 값을 추출해야 합니다.

fn do_something_with_foo(foo: Foo) {
	// switch문과 비슷한데 패턴 매칭을 해줍니다.
	match foo {
		Foo::One => println!("One"),
		// Foo::Two 팔에서 x는 i32입니다.
		Foo::Two(x) => println!("Two with {}", x),
		// Foo::Three 팔에서 x는 char입니다.
		Foo::Three(x) => println!("Three with {}", x),
		Foo::Four(x, y) => println!("Four with {} and {}", x, y),
	}
}

합 타입도 원소의 개수를 논해볼 수 있고, 이미 예상하셨듯이 \(\lvert A + B \rvert = \lvert A \rvert + \lvert B \rvert\)가 성립합니다. 집합론적 관점에서는 분리합집합에 해당하는데, 보통의 합집합과 달리 공통으로 포함된 원소가 합쳐지지 않습니다.

곱셈이 덧셈의 연속인 것처럼 생각할 수 있듯이, 곱 타입 \(A \times B\)도 \(\lvert A \rvert\)개의 선택지가 각각 \(B\)를 하나씩 들고 있는 것으로 생각할 수도 있습니다(\(B + B + B + \cdots + B\)).

괄호 안에는 아까 보았던 튜플 타입처럼 여러 타입을 집어넣어도 됩니다. 이 관점에서 보면 enum은 합 타입에 곱 타입을 약간 섞은 느낌이네요.

아쉽게도 Rust에는 enum을 만들지 않는 "가벼운" 합 타입 문법이 없습니다. 혹시 곱 타입에서처럼 선택지를 2개 미만으로 넣을 수 있을까요?

// i32와 같은 타입입니다.
enum OneEnumI32 { // = i32
	One(i32),
}

// ()와 같이 값을 하나만 가집니다.
// 아래의 열거자 One은 `One(),`에서 괄호가 생략된 것으로 볼 수도 있습니다.
enum OneEnumUnit { // = 1
	One,
}

enum ZeroEnum {} // ???????

타입 0개의 합도 있을 수 있습니다. 예를 들어, ZeroEnum은 값을 가질 수 없는 타입입니다. 단위 타입 1은 값이 하나라도 있었지만, ZeroEnum은 말 그대로 만들 수도, 저장할 수도, 연산할 수도 없습니다. ZeroEnum을 "반환하는" 함수는 절대 값을 반환할 수 없고, 무한루프를 돌든지 panic!을 일으키든지 해야 합니다.

이런 타입을 바닥 타입이라고도 하는데, 합 타입의 항등원이자 곱 타입의 흡수원1으로 작용합니다. 예를 들면...

// `!`는 Rust에서 기본 지원하는 바닥 타입으로, "never"라고 읽습니다.
// 이 글을 쓰는 시점에서 이 타입은 아직 지원이 불안정하기 때문에
// 실제 코드에는 사용할 수 없습니다.

// i32와 같은 타입입니다.
enum EnumPlusZero { // = i32 + 0 = i32
	One(i32),
	Two(!),
}

// !와 같은 타입입니다.
struct TupleTimesZero(i32, !); // i32×0 = 0

아까 곱의 항등원 타입을 1로 쓰기로 했으니 바닥 타입도 0으로 표기하겠습니다(정수 0이 아님에 유의).

삼천포: 거듭제곱 타입

이 글에서 필요하지는 않지만 흥미로운 내용이라서 추가하겠습니다.

아까 합 타입을 설명할 때 \(A \times B\)를 \(B + B + B + \cdots + B\)로 나타낼 수 있다고 했었죠? 여기서 모든 \(+\)을 \(\times\)으로 바꾸면 \(B\)를 \(\lvert A \rvert\)개 들고 있다는 의미가 되고, 편의상 \(B^A\)로 표기할 수 있습니다. 이 \(\lvert A \rvert\)개의 \(B\) 중 하나를 \(A\) 하나로 특정하는 문법을 생각해볼 수 있습니다.

let group_of_b: B^A = /* TODO */;
let a: A = /* TODO */;
let b: B = group_of_b[a];

여기서 대괄호만 소괄호로 바꾸면...

let b: B = group_of_b(a);

\(B^A\)는 다름이 아니라 \(A\)를 받아서 \(B\)를 내놓는 함수 타입인 것을 알 수 있습니다. 마침 집합 \(A\)에서 \(B\)로 가는 함수도 \(\lvert B \rvert^{\lvert A \rvert}\)개 있네요. 아쉽지만 거듭제곱 타입은 Haskell 등 함수에 부작용이 없는 순수 함수형 언어에서만 성립하는 개념이라 자주 언급되지는 않습니다.

예시

대수적 자료형을 사용하는 예시는 얼마든지 많이 있지만, 제가 당장 기억나는 것 중 하나가 플레잉 카드입니다. 아마 여기서 봤던 걸 기억하고 있는 것 같습니다.

enum Suit { // = 1 + 1 + 1 + 1
	// 편의상 1 + 1 + 1 + 1 = 4라고 표기하겠습니다.
	// 정수가 아닌 타입임에 유의해 주세요.
	Club,
	Diamond,
	Heart,
	Spade,
}

enum Rank { // = 1 + 1 + ... + 1 = 13
	Ace,  Two,   Three, Four, Five,
	Six,  Seven, Eight, Nine, Ten,
	Jack, Queen, King,
}

enum Joker { // = 1 + 1 = 2
	Black,
	Red,
}

enum PlayingCard { // = 2 + 4×13
	Joker(Joker),
	NonJoker(Suit, Rank),
}

Rust의 표준 라이브러리에 있는 것으로 예시를 들자면, 값이 없을 수도 있음을 표현하는 Option 타입이 있습니다.

// <T>는 템플릿/제네릭 문법입니다.
enum Option<T> { // = 1 + T
	None,
	Some(T),
}

type Foo = Option<(i32, char)>; // = 1 + i32×char

그러고 보니까 아까 위키백과 글에서 이진 트리의 타입을 뭐라고 했었죠?

… 예를 들어, 타입 A의 값을 담고 있는 이진 트리의 타입 T는 사상 1+A×T² → T로 생성되는 대수로 나타낼 수 있다.

… For example, the type T of binary trees containing values of type A can be represented as the algebra generated by the transformation 1+A×T² → T.

이제 대수적 자료형을 배웠으니 1+A×T²가 무슨 타입인지 표현해볼 수 있겠네요.

enum BinaryTree<A> { // = 1 + A×T×T
	Leaf,
	// 실제로 이렇게 쓰면 재귀 타입이 되기 때문에
	// BinaryTree<A> 대신 Box<BinaryTree<A>>를 써야 합니다.
	// 주제에 집중하기 위해 이 글에서는 가능하다고 치고 무시하겠습니다.
	// 참고로 Box<T>는 C++의 std::unique_ptr<T>와 같습니다.
	Node(A, BinaryTree<A>, BinaryTree<A>),
}

대수적 자료형의 성질

미분 얘기로 넘어가기 전에 대수적 자료형이 만족하는 성질을 요약하고 넘어가겠습니다. 위에서 언급하지 않은 것을 포함할 수 있습니다.

그래서 타입을 미분한다고요?

사실 이 "미분"이라는 개념이 고등학교에서 배우는 것과 조금 다르긴 합니다. 추상대수학에서 정의하는 "도함수"는 다음 성질을 만족하는 연산입니다.

그냥 미분의 성질을 늘어놓은 것 아니냐고 할 수 있는데, 추상대수학에서는 말 그대로 군, 환, 체 같은 "추상적인" 개념을 주로 다루기 때문에 덧셈과 곱셈(우리에게 친숙한 덧셈/곱셈이 아니어도 됩니다)이 적당히 정의되어 있고 저 성질만 만족한다면 어떤 것이든 도함수라고 할 수 있습니다. 예를 들어서 함수가 아니라 자연수를 미분하는 산술 도함수라는 연산이 있습니다.

물론 위의 두 성질만으로는 타입의 도함수가 갑자기 생기지 않으니 일종의 "베이스 케이스"를 정의해 봅시다. 타입 T에 대한 도함수를 \(\frac{d}{dT}\)라고 하면,

이제 이진 트리의 타입 1+A×T²을 T에 대해 미분해볼 수 있습니다. 가독성을 위해 미분 연산을 \(\frac{d}{dT}\) 대신 \('\)으로 적겠습니다.

\[\begin{align} (1 + A \times T^2)' &= 1' + (A \times T^2)' \\ &= 0 + (A \times T^2)' \\ &= A' \times T^2 + A \times (T^2)' \\ &= 0 \times T^2 + A \times (T \times T)' \\ &= 0 + A \times (T' \times T + T \times T') \\ &= A \times (1 \times T + T \times 1) \\ &= A \times (T + T) \\ &= 2 \times A \times T \end{align}\]

뭔가 대강 봐도 도함수처럼 생긴 게 나왔네요. 고등학교 미분에서도 \(\frac{d}{dt} (at^2 + 1) = 2at\)였죠? 그런데 이 2×A×T라는 게 무엇을 나타내는 타입일까요?

타입 도함수의 의미

수학적 정의에서 의미를 도출하는 건 글로 어떻게 쓸지 모르겠어서 결론부터 말씀드리겠습니다. 타입 T를 타입 U로 미분한 결과는 타입 U의 값을 한 개 가지고 있을 때, 그 값을 한 개 포함하는 타입 T의 값을 유일하게 결정하는 데 필요한 정보입니다.

...덜 복잡한 타입으로 예시를 들어 보겠습니다. i32×char를 i32로 미분하면 char가 되고, i32의 값 하나를 이미 가지고 있을 때 char가 하나 있으면 i32×char를 유일하게 결정할 수 있습니다.

type Foo = (i32, char); // = i32×char
// d/d(i32) i32×char = char
type FooDeriv = char;

fn recover_foo(value: i32, deriv: FooDeriv) -> Foo {
	(value, deriv)
}

...아니면 i32×i32로도 해 봅시다.

type Foo = (i32, i32); // = i32×i32
// d/d(i32) i32×i32 = 1×i32 + i32×1 = 2×i32
// 이미 가지고 있는 `i32` 이외에 `i32`가 하나 더 필요하고,
// 이 두 개의 `i32`를 배치할 수 있는 경우의 수가 2가지입니다.
enum FooDeriv {
	Left(i32),
	Right(i32),
}

fn recover_foo(value: i32, deriv: FooDeriv) -> Foo {
	match deriv {
		FooDeriv::Left(x) => (value, x),
		FooDeriv::Right(x) => (x, value),
	}
}

아니면 위키백과 예시로 나왔던 1+A×T²는요?

// 이 선언을 추가하면 BinaryTree::Leaf를 Leaf로,
// BinaryTreeDeriv::Left를 Left로 쓸 수 있습니다.
use BinaryTree::*;
use BinaryTreeDeriv::*;

enum BinaryTree<A> {
	Leaf,
	Node(A, BinaryTree<A>, BinaryTree<A>),
}
// d/dA (1 + A×T×T) = 2×A×T
// 위의 i32×i32 예제와 같이 `A`와 `T`가 하나씩 더 필요하고,
// 이들을 배치할 수 있는 경우의 수가 2가지입니다.
// `Leaf`인 경우에는 `T`를 배치할 수 없으므로 생각하지 않습니다.
enum BinaryTreeDeriv<A> {
	Left(A, BinaryTree<A>),
	Right(A, BinaryTree<A>),
}

fn recover_binary_tree<A>(
	value: BinaryTree<A>,
	deriv: BinaryTreeDeriv<A>
) -> BinaryTree<A> {
	match deriv {
		Left(a, t) => Node(a, value, t),
		Right(a, t) => Node(a, t, value),
	}
}

타입의 "이계도함수"도 취할 수 있고, 이때는 값 2개를 가지고 있을 때 타입 T의 값을 유일하게 결정하는 데 필요한 정보가 됩니다.

type Foo = (i32, i32, i32); // T×T×T
enum FooDeriv { // d/dT T×T×T = 3×T×T
	One(i32, i32),
	Two(i32, i32),
	Three(i32, i32),
}
enum FooDeriv2 { // d^2/dT^2 T×T×T = 6×T
	OneTwo(i32),
	OneThree(i32),
	TwoOne(i32),
	TwoThree(i32),
	ThreeOne(i32),
	ThreeTwo(i32),
}

fn recover_foo(
	value1: i32,
	value2: i32,
	deriv: FooDeriv2
) -> Foo {
	match deriv {
		OneTwo(x) => (value1, value2, x),
		OneThree(x) => (value1, x, value2),
		// (생략)
		ThreeTwo(x) => (x, value2, value1),
	}
}

제가 예시를 든다고 이런저런 타입을 가져오긴 했지만, 타입의 도함수는 보통 처음 예시로 나왔던 1+A×T² → T처럼 재귀적인 타입에만 취하는 편이고, 다른 타입에 대해 미분할 수도 있지만 그렇게까지 쓸데가 있지는 않은 것 같습니다.

"쓸데"라는 단어를 언급한 걸 보니 뭔가 쓸데가 있는 모양이네요.

지퍼 자료구조

함수형 프로그래밍 언어에서 쓰이는 지퍼라는 자료구조가 있습니다. 제가 이해한 대로 최대한 쉽게 설명하려고 해본다면, "상자의 상태를 기억해둔 뒤 그 상자를 뜯고, 내용물을 쓴 뒤에 다시 원래 상태대로 상자를 포장하는 것"에 가깝습니다.

역시 개발 블로그니까 코드로 예시를 들어 보겠습니다.

enum PresentBox { // = 1 + PresentBox
	Empty,
	Full(PresentBox),
}
type PresentBoxDeriv = (); // d/d(PresentBox) (1 + PresentBox) = 1

fn unpack(present: PresentBox) -> (PresentBox, PresentBoxDeriv) {
	match present {
		// 예시니까 예외 처리 없이 터지게 짜겠습니다.
		PresentBox::Empty => panic!(),
		PresentBox::Full(content) => (content, ()),
	}
}
fn pack(content: PresentBox, deriv: PresentBoxDeriv) -> PresentBox {
	PresentBox::Full(content)
}
fn use_content(content: &mut PresentBox) {
	// 예시 함수입니다.
}

// 3겹짜리 상자
let my_box = PresentBox::Full(
	PresentBox::Full(
		PresentBox::Empty
	)
);
// 1겹의 포장을 뜯고
// 내용물은 unpacked_box, 껍데기는 box_state에 저장합니다.
let (mut unpacked_box, box_state) = unpack(my_box);
// 내용물을 쓴 뒤에...
use_content(&mut unpacked_box);
// 껍데기를 다시 가져와서 원래대로 포장합니다.
let repacked_box = pack(unpacked_box, box_state);

...하지만 PresentBox가 재귀적 타입인 것을 감안해 스택을 만들어서 거기에 상태를 쌓아두는 것이 더 편합니다. 이렇게 하면 껍데기 여러 겹을 한 곳에 모아둘 수 있습니다.

struct PresentBoxZipper {
	content: PresentBox,
	stack: Vec<PresentBoxDeriv>,
}

fn unpack_z(mut zipper: PresentBoxZipper) -> PresentBoxZipper {
	let (new_box, new_state) = unpack(zipper.content);
	zipper.stack.push(new_state);
	PresentBoxZipper {
		content: new_box,
		stack: zipper.stack,
	}
}
fn pack_z(mut zipper: PresentBoxZipper) -> PresentBoxZipper {
	// 이것도 어차피 예시니까
	// zipper.stack이 비어 있지 않다고 가정합니다.
	// .pop()은 아까 보았던 Option을 리턴하기 때문에
	// 값을 꺼내려면 .unwrap() 등 무언가 추가로 연산을 해야 합니다.
	let pack_state = zipper.stack.pop().unwrap();
	PresentBoxZipper {
		content: pack(zipper.content, pack_state),
		stack: zipper.stack,
	}
}

// 3겹짜리 상자. 초기에는 쌓인 껍데기가 없습니다.
let mut zipper = PresentBoxZipper {
	content: PresentBox::Full(
		PresentBox::Full(
			PresentBox::Empty
		)
	),
	stack: vec![],
};
// 2겹의 포장을 뜯고 껍데기를 스택에 넣어둡니다.
zipper = unpack_z(zipper);
zipper = unpack_z(zipper);
// 내용물을 쓴 뒤에...
use_content(&mut zipper.content);
// 스택에서 껍데기를 꺼내서 원래대로 포장합니다.
zipper = pack_z(zipper);
zipper = pack_z(zipper);

상자를 뜯지 말고 그냥 안쪽의 포인터/참조를 넘겨주면 안 되느냐고 생각할 수 있지만, 값을 한 번 만들면 절대 수정할 수 없는 환경에서는 이 방식이 참조 넘겨주기보다 더 편하고 그런 환경의 대표적인 예시가 함수형 프로그래밍입니다. 대수적 자료형도 함수형 언어에서 자주 쓰이는 걸 생각해보면 절대 우연은 아닌 것 같네요. 위의 코드 예시에서는 mut2을 적당히 사용했지만, 불변 값만 사용해서도 지퍼를 구현할 수 있습니다.

정규식도 미분할 수 있을까?

여기까지가 원본 위키백과 문서에서 설명하고 있는 내용입니다. 그런데 이미 여기까지 와버렸고 글을 여기서 마칠 수 없는 저는 무언가 또 이상한 걸 해보기로 했습니다.

곱의 미분법만 성립하면 도함수라고? 그러면 정규식도 미분할 수 있을까?

빠른 예습/복습

대수적 자료형을 설명하는 데 <h1> 하나를 할애했으니 여기서는 정규식이 뭔지 간단히만 훑어보도록 하겠습니다.

정규 표현식(regular expression, 줄여서 정규식)은 원하는 규칙의 문자열을 찾는 데 사용하는 도구입니다. 원래 정규식으로는 정규 언어라는 것만을 표현할 수 있지만, 정규식이 꽤나 유용하다 보니 정규 언어가 아닌 것을 찾을 수 있도록 기능을 확장한 정규식 엔진도 자주 볼 수 있습니다. 이 글에서는 원래 의미의 정규식만을 다룹니다.

입력으로 들어올 수 있는 모든 문자를 알파벳이라고 하는데, 정규 표현식은 알파벳을 그대로 사용하거나(정확히 그 알파벳 하나를 찾습니다) 다음 방식대로 연산해서 만들 수 있습니다.

"덧셈"

이 연산자를 한국어로 뭐라고 부르는지 모르겠으니 그냥 따옴표를 써서 "덧셈"이라고 부르겠습니다.

두 정규식을 "덧셈"할 수 있고, 기호는 |입니다. 둘 중 하나라도 일치하면 전체 식이 일치합니다. 예를 들어서 gray|grey는 gray나 grey를 찾고 gr(a|e)y와 같습니다.

"덧셈"이라고 하는 것에서 알아보셨겠지만 이 연산자는 덧셈의 역할을 합니다. 항등원의 역할을 하는 정규식은 "공집합" 정규식 ∅으로, 아무것도 찾지 않습니다. 아까 바닥 타입은 0이라고 썼었지만, 정규식에서는 0이나 1을 알파벳으로 쓸 수도 있으므로 그냥 이대로 쓰겠습니다.

연결

두 정규식을 연결할 수 있고, 별도의 기호는 없습니다. 두 식이 차례대로 일치해야 전체 식이 일치합니다. 예를 들어서 gray는 네 정규식 g, r, a, y를 연결한 것으로 볼 수 있고 gray를 찾습니다.

이 연산자는 곱셈의 역할을 합니다. 항등원의 역할을 하는 정규식은 "빈 문자열" 정규식 ε으로, 빈 문자열을 찾습니다. 바닥 타입과 단위 타입이 미묘하게 달랐던 것처럼 ∅과 ε도 미묘하게 다른데, ∅과 일치하는 문자열은 0개, ε과 일치하는 문자열은 빈 문자열 1개입니다.

클레이니 스타

정규식에 클레이니 스타를 붙일 수 있습니다. 정규식 \(R\)에 대해 \(R^*\)은 \(\epsilon\), \(R\), \(RR\), \(RRR\), \(RRRR\), ...과 모두 일치합니다. 예를 들어서 (ab)*는 빈 문자열을 포함해 ab, abab, ababab, abababab, ...를 모두 찾습니다.

이외에 편의상 다음 연산자나 문법을 추가로 도입하기도 합니다.

정규 표현식의 성질

정규식의 도함수 정의하기

곱셈의 교환법칙을 제외하고 아까 보았던 대수적 자료형의 성질을 모두 만족하니 도함수를 정의해도 문제가 없을 것 같네요.

도함수란 다음 성질을 만족하는 연산이라고 했었습니다.

아까 타입에 했던 것처럼 베이스 케이스를 만들어 봅시다. 알파벳 \(a\)에 대한 도함수를 \(\frac{d}{da}\)라고 하면,

클레이니 스타의 미분법을 아직 정하지 않았는데, 일단 ε|aa* = a*의 양변을 미분하면서 생각해 봅시다.

\[\begin{align} (a^*)' &= (\epsilon | aa^*)' \\ &= \epsilon' | (aa^*)' \\ &= \emptyset | a'a^* | a(a^*)' \\ &= \epsilon a^* | a(a^*)' \\ &= a^* | a(a^*)' \end{align}\]

이제 우변의 \((a^*)'\)에 우변 전체를 계속 대입하면...

\[\begin{align} (a^*)' &= a^* | a(a^*)' \\ &= a^* | a(a^* | a(a^*)') \\ &= a^* | aa^* | aa(a^*)' \\ &= a^* | aa^* | aa(a^* | aa^* | aa(a^*)') \\ &= a^* | aa^* | aaa^* | aaaa^* | aaaa(a^*)' \\ &= \cdots \\ &= (\epsilon | a | aa | aaa | ...)a^* \\ &= a^*a^* \\ &= a^* \end{align}\]

제가 도함수를 모순 없이 잘 정의했는지는 잘 모르겠네요. 일단 이 정의를 따른다면, 정규식의 알파벳 a에 대한 도함수는 그 정규식과 일치하는 모든 문자열에서 임의로 a를 하나 뺀 모든 문자열을 찾는 정규식입니다.

이걸 실용적으로 쓸 수 있을지는 잘 모르겠네요. 알파벳이 아니라 임의의 정규식에 대해서도 비슷한 걸 만들어보고 싶은데 그렇게는 안 되는 것 같습니다.

앞으로도 신기한 걸 찾으면 혼자만 알고 있기 재미없으니 블로그에 #TIL을 붙여서 올릴 것 같습니다. 글을 쓰면서 뭔가 아는 척을 계속 하긴 했는데 저도 잘 모르는 분야이기 때문에 잘못된 점에 대한 제보는 감사히 받겠습니다. 감사합니다 🙇‍♂️

  1. Absorbing element. 어떤 집합 \(S\)와 연산 \(*\)이 있을 때, \(S\)의 모든 원소 \(x\)에 대해 \(x * e = e * x = e\)를 만족하는 \(e \in S\)를 말합니다. ↩

  2. const를 추가해야 값이 불변이 되는 C와 달리, Rust는 값이 불변인 것이 기본값이고 mut을 추가해야 값을 수정할 수 있습니다. 참조 역시 값을 수정할 수 없는 &와 수정할 수 있는 &mut으로 나뉩니다. ↩

타입을 미분할 수 있다고?