제가 백준 14939번 "불 끄기"를 무슨 역행렬을 쓰는 이상한 방법으로는 풀 수 있는데 브루트포스로 푸는 방법은 최근까지 전혀 몰랐다고 하면 믿어지시나요? 저도 못 믿겠습니다.

아무튼 이 글은 Honeyhouse와 한별포스 이후 벌써 3번째로 작성하는 선형대수학에 관한 글입니다. 분량은 그렇게까지 길어지지는 않을 것 같네요.

문제 옮겨적기

문제

전구 100개가 10×10 정사각형 모양으로 늘어서 있다. 전구에 달린 스위치를 누르면 그 전구와 위, 아래, 왼쪽, 오른쪽에 있는 전구의 상태도 바뀐다. 전구 100개의 상태가 주어지면 모든 전구를 끄기 위해 최소한으로 눌러야 하는 스위치의 개수를 출력하라

입력

10줄에 10글자씩 입력이 주어진다. #은 꺼진 전구고 O(대문자 알파벳 o)는 켜진 전구다. #과 O외에는 입력으로 주어지지 않는다.

출력

모든 전구를 끄기 위해 최소한으로 눌러야 하는 스위치의 개수를 출력하라. 불가능하면 -1를 출력하라.

예제 입력 1

#O########
OOO#######
#O########
####OO####
###O##O###
####OO####
##########
########O#
#######OOO
########O#

예제 출력 1

4

작은 버전의 문제

때마침 설명에 쓰기 좋은 게임이 있네요. 프로토 게임잼¹ 2022년 4월 참여작인 도바's 캔디드롭을 소개합니다.

플레이어가 원형의 아레나 위를 돌아다니고, 가운데에 보스가 있습니다(오른쪽 위의 원 모양 그림이 위에서 본 미니맵입니다). 보스의 공격을 적당히 피하면서 아레나에 설치된 버튼 8개를 모두 눌러진(노란색) 상태로 바꾸어야 하는데, 버튼을 누르면 양옆 버튼의 상태가 같이 바뀝니다. 원본 문제와는 달리 양옆이 연결되지만 일단은 신경쓰지 말아 봅시다.

이 게임이 올라왔을 당시에 스피드런 이벤트가 같이 열리고 있었는데, 가끔씩 처음 보는 헷갈리는 버튼 조합이 나와서 시간을 다 잡아먹길래 머릿속에서 계산할 수 있는 공략법이 있는지 자연스럽게 생각해보게 되었습니다. 지금도 디스코드에 이 흔적이 남아 있습니다.

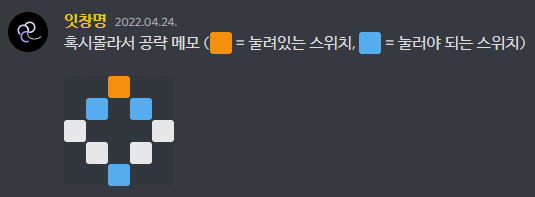
반응 행렬 만들기

버튼에 1번부터 8번까지 번호를 붙이고 각 버튼이 어떻게 상호작용하는지 반응 행렬(급조한 이름입니다)로 나타내 봅시다. 이 행렬의 원소 $\mathbf{R}_{ij}$는 $i$번째 버튼을 눌렀을 때 $j$번째 버튼이 반응하면 1, 그렇지 않으면 0입니다.

$$\mathbf{R} = \begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 & 1 & 1 \end{pmatrix}$$

이 행렬의 오른쪽에 누르려는 버튼을 열벡터로 모아서 곱하면 버튼을 누른 결과를 나타내는 열벡터를 얻을 수 있습니다.

$$\mathbf{R} \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{pmatrix}$$

그런데 제가 원하는 건 원하는 결과가 주어졌을 때 올바른 버튼의 조합을 구하는 것입니다. 완전히 반대 방향이네요. 역행렬을 구해 봅시다!

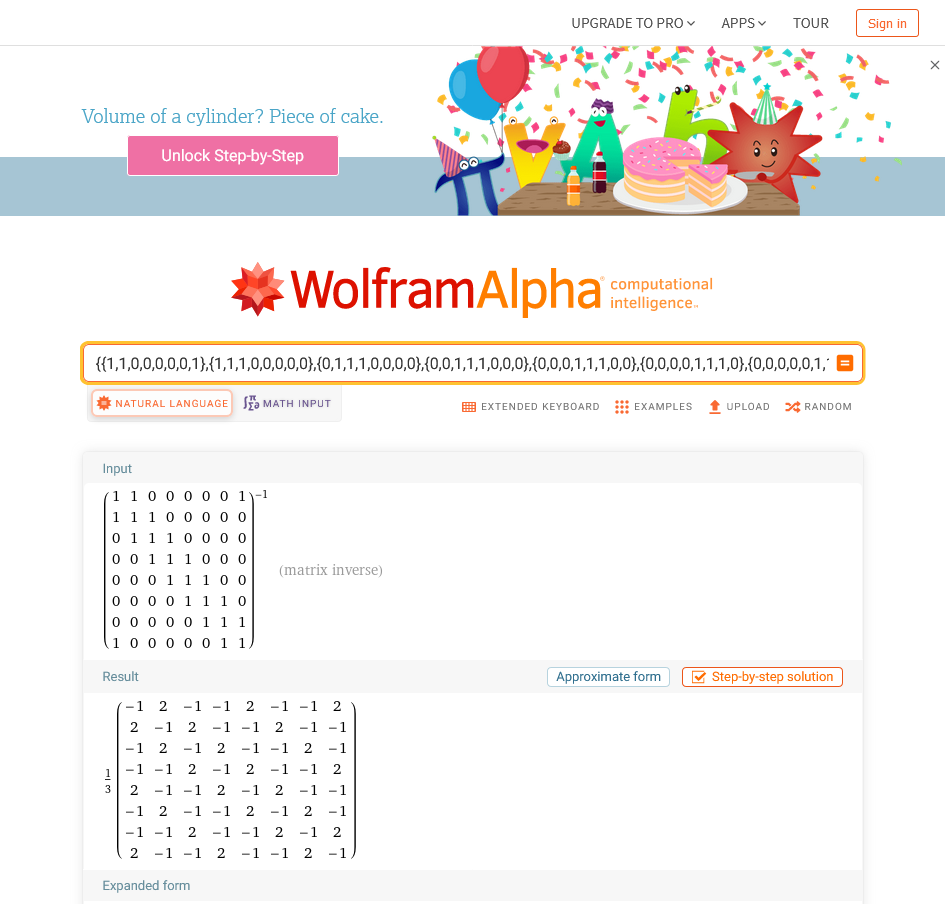
어... 잠시 혼선이 있었습니다. 대신 직접 구한 결과는 이렇습니다.

$$\mathbf{R}^{-1} = \begin{pmatrix} 1 & 0 & 1 & 1 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 & 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 & 1 & 1 & 0 & 1 \end{pmatrix}$$

검산 겸 위에서 $\mathbf{R}^{-1}$에 2번, 5번, 8번 버튼을 누른 결과를 다시 곱해봅시다.

$$\mathbf{R}^{-1} \begin{pmatrix} 0 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 1 \end{pmatrix}$$

눌러야 되는 버튼 조합을 복구했네요! 위의 $\mathbf{R}^{-1}$을 뜷어져라 쳐다보면, 누르고 싶은 버튼이 있으면 그 버튼을 포함해서 좌우 2칸, 3칸씩 떨어진 버튼(총 5개입니다)을 전부 누르면 된다는 공략을 얻을 수 있습니다. 머릿속으로 계산하기 어려운 공략이긴 하네요.

실수 행렬과 0-1 행렬

위에서 Wolfram|Alpha로 계산한 결과를 다시 보면 처음에 예상했던 0과 1의 조합이 아니라 $-\frac{1}{3}$과 $\frac{2}{3}$의 범벅이었습니다. 뭐가 문제였을까요?

사실 "처음에 예상했던 0과 1의 조합"에 제가 말하지 않고 넘어갔던 가정이 숨어 있습니다. 행렬 $\mathbf{R}$은 임의의 실수가 아니라 0과 1만으로 이루어진 0-1 행렬입니다. 게다가 우리는 누른 버튼을 다시 누르면 원래대로 돌아온다는, 즉 1+1=0이라는 가정을 추가로 하고 있었습니다. Wolfram|Alpha는 대신 $\mathbf{R}$이 일반적인 실수 행렬이라고 가정하고 풀었기 때문에 "잘못된"² 결과가 나온 것입니다.

그러고 보니까 창명님, 혹시 아까 $\mathbf{R}^{-1}$은 어떻게 구하셨나요?

그냥 가우스 소거법 썼는데요?

엥? 일반적인 실수 행렬도 아닌데 그래도 되나요?

추상 벡터 공간

그럴 줄 알고 수학자들이 이미 벡터와 행렬을 일반화해서 벡터 공간이라는 이름을 붙여 놓았습니다. 다음과 같은 몇 가지 공리만 만족시키면 "벡터 공간"이라고 하고, 선형대수학의 모든 정리와 도구를 그냥 가져와서 쓸 수 있습니다.

설명의 편의상 스칼라는 기울임꼴 소문자, 벡터는 굵은 소문자, 행렬은 굵은 대문자로 적겠습니다.

• 스칼라가 체를 이룬다.
  • 덧셈의 결합법칙: $a + (b + c) = (a + b) + c$
  • 덧셈의 교환법칙: $a + b = b + a$
  • 덧셈의 항등원의 존재: $a + 0 = a$
  • 덧셈의 역원의 존재: $a + (-a) = 0$
  • 곱셈의 결합법칙: $a \cdot (b \cdot c) = (a \cdot b) \cdot c$
  • 곱셈의 교환법칙: $a \cdot b = b \cdot a$
  • 곱셈의 항등원의 존재: $a \cdot 1 = a$
  • 곱셈의 역원의 존재: $a \cdot a^{-1} = 1$ (단, $a \ne 0$)
  • 덧셈에 대한 곱셈의 분배법칙: $a \cdot (b + c) = a \cdot b + a \cdot c$
  • 이건 공리라기보다는 전제 조건에 가까운 느낌으로 들어가 있습니다.
• 벡터 공간의 8대 공리
  • 벡터합의 결합법칙: $\mathbf{u} + (\mathbf{v} + \mathbf{w}) = (\mathbf{u} + \mathbf{v}) + \mathbf{w}$
  • 벡터합의 교환법칙: $\mathbf{u} + \mathbf{v} = \mathbf{v} + \mathbf{u}$
  • 벡터합의 항등원의 존재: $\mathbf{v} + \mathbf{0} = \mathbf{v}$
  • 벡터합의 역원의 존재: $\mathbf{v} + (-\mathbf{v}) = \mathbf{0}$
  • 곱셈과 스칼라곱의 호환성: $a \cdot (b \cdot \mathbf{v}) = (a \cdot b) \cdot \mathbf{v}$
  • 스칼라곱의 항등원의 존재: $1 \cdot \mathbf{v} = \mathbf{v}$
    • 여기서의 $1$은 위에서 언급한 곱셈의 항등원과 같습니다.
  • 벡터합에 대한 스칼라곱의 분배법칙: $a \cdot (\mathbf{u} + \mathbf{v}) = a \cdot \mathbf{u} + a \cdot \mathbf{v}$
  • 덧셈에 대한 스칼라곱의 분배법칙: $(a \cdot b) \cdot \mathbf{v} = a \cdot \mathbf{v} + b \cdot \mathbf{v}$

뭔가 내용이 엄청나게 많아 보이는데 제가 전부 풀어서 써서 그렇지 공리 하나하나는 생각보다 어렵지 않습니다. 여기서 중요한 점은, 관례상 덧셈과 벡터합을 $+$, 곱셈과 스칼라곱을 $\cdot$, 덧셈의 항등원을 $0$, 곱셈의 항등원을 $1$로 쓰긴 했지만 이것들이 진짜로 덧셈, 곱셈, 0, 1이 아니어도 된다는 것입니다. 애초에 이 문제에서는 1 더하기 1이 0입니다.

제가 이 이상 설명하려고 하면 더 이해하기 어려워질 것 같으니 나머지는 3Blue1Brown님의 이 유튜브 동영상으로 넘기겠습니다. 원래 이 글에서 0-1 벡터가 왜 벡터 공간을 이루는지도 전부 유도해보려고 했는데, 쓰기도 재미없고 읽기도 재미없을 것 같으니 연습문제로 남기겠습니다. 결론만 정리하자면 다음과 같습니다.

• 스칼라는 0과 1로만 이루어져 있음
• 덧셈은 모듈로 2 덧셈
  • 덧셈의 항등원은 0
• 곱셈은 일반 곱셈
  • 곱셈의 항등원은 1

아니면 이렇게도 해석할 수 있고, 어느 관점을 취하든 상관은 없습니다.

• 스칼라는 참과 거짓으로만 이루어져 있음
• 덧셈은 배타적 논리합 (XOR)
  • 덧셈의 항등원은 거짓
• 곱셈은 논리곱 (AND)
  • 곱셈의 항등원은 참

실전 문제 풀기

이제 문제를 푸는 방법도 알았고 그 방법이 올바르다는 것도 알았으니 실제로 문제를 풀어볼 시간입니다.

반응 행렬 만들기

도바's 캔디드롭에서는 버튼이 8개밖에 없었지만, 이 문제에서는 스위치가 무려 100개이고 반응 행렬도 100×100짜리가 됩니다. 이 정도는 컴퓨터로 비교적 빨리 풀 수 있으니 상관 없긴 합니다. 편의상 스위치 번호는 줄글을 읽듯이 붙입시다.

반응 행렬은 적당한 언어에서 100×100짜리 이차원 배열을 만들고 각 줄마다 자신과 상하좌우에 해당하는 원소를 찾아 1로 만들면 됩니다. 저는 C++로 짰습니다.

역행렬 구하기

...그런데 여기서 잠깐, 반응 행렬이 가역이라고 확신할 수 있나요?

RREF 구하기

아까 가우스 소거법을 썼다고 잠깐 언급했는데, 가우스 소거법으로 역행렬 $\mathbf{R}^{-1}$을 구하는 방법은 이렇습니다.

우선 $\mathbf{R}$과 $\mathbf{I}$로 첨가행렬을 만듭니다.

$$\left( \begin{array}{c|c} \mathbf{R} & \mathbf{I} \end{array} \right)$$

이 행렬의 RREF를 구해서 왼쪽 절반이 $\mathbf{I}$가 된다면 나머지 오른쪽이 $\mathbf{R}$의 역행렬입니다.

이게 왜 성립하나요?

RREF나 가우스 소거법이 정확히 뭐고 어떻게 하는 건지는 이 글에서는 생략하지만, 연립방정식의 모양을 바꾸면서 해는 바꾸지 않는 연산을 여러 번 해서 예쁘게 만드는 것이라고만 하겠습니다.

저번 한별포스 글에서 "행렬로 연립 일차방정식도 풀 수 있다"고 했었는데, 보통 행렬로 연립방정식을 풀 때는 식을 이런 꼴로 세우고...

$$\mathbf{A}\mathbf{v} = \mathbf{b}$$

연립방정식의 관점에서는 이렇게 볼 수 있습니다.

• $\mathbf{A}_{11}\mathbf{v}_1 + \mathbf{A}_{12}\mathbf{v}_2 + \mathbf{A}_{13}\mathbf{v}_3 + \cdots = \mathbf{b}_1$
• $\mathbf{A}_{21}\mathbf{v}_1 + \mathbf{A}_{22}\mathbf{v}_2 + \mathbf{A}_{23}\mathbf{v}_3 + \cdots = \mathbf{b}_2$
• $\mathbf{A}_{31}\mathbf{v}_1 + \mathbf{A}_{32}\mathbf{v}_2 + \mathbf{A}_{33}\mathbf{v}_3 + \cdots = \mathbf{b}_3$
• ...

또 이걸 풀 때는 아까처럼 $\mathbf{A}$와 $\mathbf{b}$로 첨가행렬을 만들어서 RREF를 구합니다.

$$\left( \begin{array}{c|c} \mathbf{A} & \mathbf{b} \end{array} \right)$$

그런데 첨가행렬을 열벡터 하나 대신 행렬을 통째로 넣어서 만들면 우변에도 문자가 여러 개 생기는 효과를 가집니다. $\mathbf{u}$는 모양을 맞추기 위해 새로 만든 열벡터입니다.

$$\mathbf{A}\mathbf{v} = \mathbf{B}\mathbf{u}$$ $$\left( \begin{array}{c|c} \mathbf{A} & \mathbf{B} \end{array} \right)$$

• $\mathbf{A}_{11}\mathbf{v}_1 + \mathbf{A}_{12}\mathbf{v}_2 + \mathbf{A}_{13}\mathbf{v}_3 + \cdots = \mathbf{B}_{11}\mathbf{u}_1 + \mathbf{B}_{12}\mathbf{u}_2 + \mathbf{B}_{13}\mathbf{u}_3 + \cdots$
• $\mathbf{A}_{21}\mathbf{v}_1 + \mathbf{A}_{22}\mathbf{v}_2 + \mathbf{A}_{23}\mathbf{v}_3 + \cdots = \mathbf{B}_{21}\mathbf{u}_1 + \mathbf{B}_{22}\mathbf{u}_2 + \mathbf{B}_{23}\mathbf{u}_3 + \cdots$
• $\mathbf{A}_{31}\mathbf{v}_1 + \mathbf{A}_{32}\mathbf{v}_2 + \mathbf{A}_{33}\mathbf{v}_3 + \cdots = \mathbf{B}_{31}\mathbf{u}_1 + \mathbf{B}_{32}\mathbf{u}_2 + \mathbf{B}_{33}\mathbf{u}_3 + \cdots$
• ...

그런데 $\mathbf{B}$의 자리에 대신 $\mathbf{I}$를 넣으면...

$$\mathbf{A}\mathbf{v} = \mathbf{I}\mathbf{u} = \mathbf{u}$$ $$\left( \begin{array}{c|c} \mathbf{A} & \mathbf{I} \end{array} \right)$$

• $\mathbf{A}_{11}\mathbf{v}_1 + \mathbf{A}_{12}\mathbf{v}_2 + \mathbf{A}_{13}\mathbf{v}_3 + \cdots = \mathbf{u}_1$
• $\mathbf{A}_{21}\mathbf{v}_1 + \mathbf{A}_{22}\mathbf{v}_2 + \mathbf{A}_{23}\mathbf{v}_3 + \cdots = \mathbf{u}_2$
• $\mathbf{A}_{31}\mathbf{v}_1 + \mathbf{A}_{32}\mathbf{v}_2 + \mathbf{A}_{33}\mathbf{v}_3 + \cdots = \mathbf{u}_3$
• ...

원점으로 돌아왔다고요? 그런데 잘 생각해보면, 우변이 상수 $\mathbf{b}_i$ 대신 미지수 $\mathbf{u}_i$로 달라졌습니다. 다르게 말하면, 이 첨가행렬을 RREF하면 $\mathbf{A}$(좌변)를 고정하고 모든 $\mathbf{u}$(우변)에 대해서 연립방정식을 푸는 것과 같습니다. 와!

역행렬이 없다면?

그런데 만약에 왼쪽 절반이 $\mathbf{I}$가 아니라면 어떻게 될까요? 이럴 때는 "역행렬이 존재하지 않는다"고 하고, 연립방정식 관점에서는 각 줄마다 무슨 모양인지 살펴봐야 하는데, 보통 이 두 가지 패턴을 조심하면 됩니다.

• 좌변에 항이 2개 이상 있음 ($\mathbf{v}_1 + \mathbf{v}_2 = \mathbf{u}_1 + \mathbf{u}_3 + \cdots$)
  • 우변의 여러 항을 좌변에 아무렇게나 나눠서 넣으면 되는데, 가장 첫 항을 잡아서 전부 몰아넣고 나머지는 0으로 놓는 게 제일 편합니다.
• 좌변이 0임 ($0 = \mathbf{u}_2 + \mathbf{u}_5 + \cdots$)
  • 이 식이 성립하지 않으면 연립방정식의 해가 존재하지 않습니다.

역으로 역행렬이 존재한다면 연립방정식의 해가 반드시 하나 존재한다고 말할 수 있습니다.

이 점을 염두에 두면서 위에서 구한 반응 행렬에 RREF를 하고 결과를 확인해 봅시다. 역행렬이 있는지 없는지를 여기서 밝히면 문제를 푸는 재미가 없으니 비밀로 하겠습니다. 저는 결과를 구해서 Base64로 인코딩한 뒤 제출하는 코드에 하드코딩으로 넣었습니다(🤣).

정답 구하기

위에서 하드코딩한 행렬을 디코딩하고 입력으로 받은 전구 상태를 방정식 100개에 각각 넣어서 계산하고 나면 위에서 잠깐 보았듯이 세 가지 경우로 나눌 수 있습니다.

• 좌변에 항이 정확히 1개 있음 ($\mathbf{v}_1 = 1$)
  • 우변을 스위치 개수에 그대로 반영하면 됩니다.
• 좌변에 항이 2개 이상 있음 ($\mathbf{v}_3 + \mathbf{v}_5 = 0$)
  • 어차피 하나 빼고 나머지는 0으로 처리하면 되니 똑같이 반영하면 됩니다.
• 좌변이 0임
  • $0 = 0$이면 그냥 무시하면 됩니다.
  • $0 = 1$이면 모든 전구를 끌 수 있는 방법이 없으므로 -1을 출력하고 종료합니다.

역행렬이 존재한다면 $\mathbf{R}^{-1}$만 하드코딩하고 첫 번째 경우만 고려하면 되니 풀기 훨씬 쉬워집니다.

첫 문단에서 얘기했듯이 이거는 제가 이상한 방법을 생각해서 어거지로 푼 것에 조금 더 가까우니 이 방법 대신 "제대로 된" 풀이법으로 푸는 것을 권장드립니다. 저도 글을 올리고 나서 제대로 풀어볼 예정입니다.

글의 주제와 전혀 무관한 여담

저는 스피드런 이벤트에서 개발자 제외 2등을 해서 상품을 받았습니다. 제 기록이 궁금하신가요? (스포일러 주의)

1. 제가 참여하고 있는, 1달에 한 번씩 게임잼을 여는 디스코드 그룹입니다. 글이 살짝 홍보에 가까워지는 것 같긴 한데 에라 모르겠네요. ↩

2. 사실 완전히 잘못된 것은 아닌 게, 모든 원소에 $\mathrm{mod} \; 2$ 연산을 하면 올바른 0-1 행렬인 $\mathbf{R}^{-1}$을 얻을 수 있습니다. 자세한 내용은 다른 글에 정리해 두었습니다. ↩